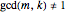Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Fourier Construction of Regular Polygons and Star Polygons

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

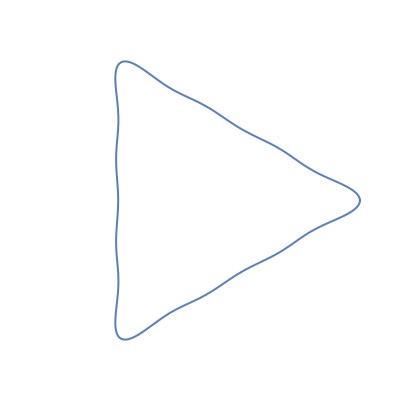
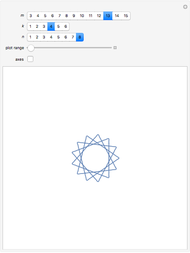
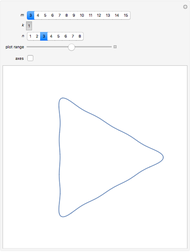
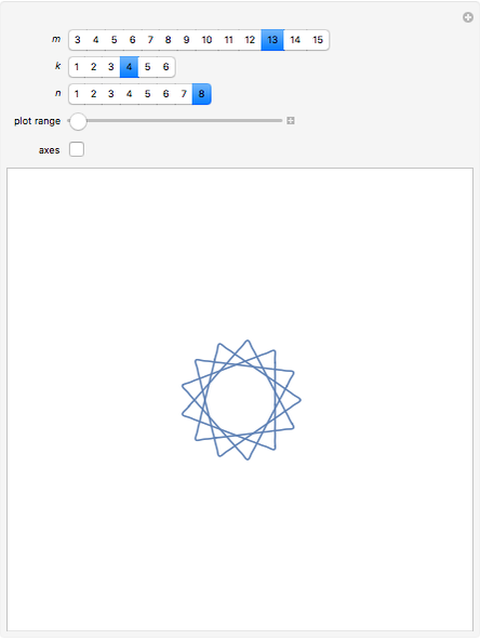
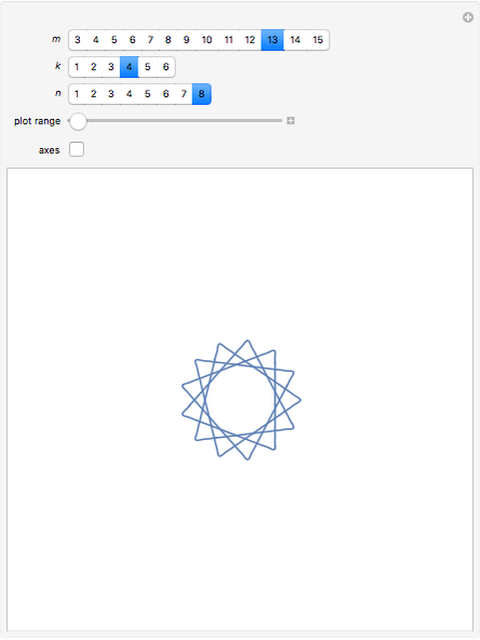
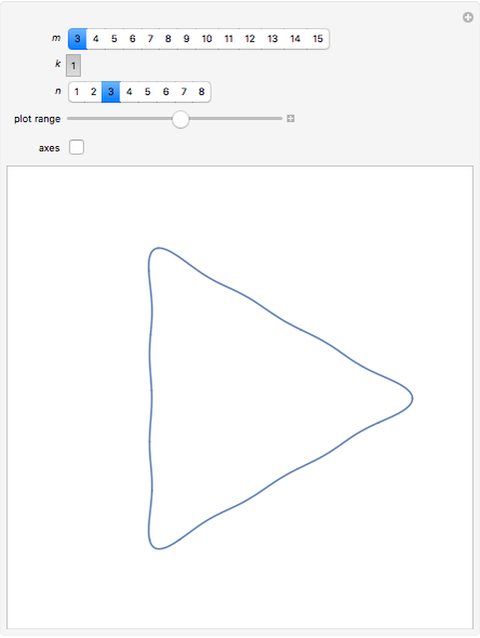
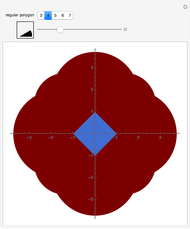
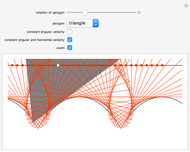
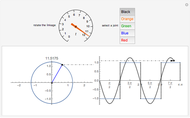
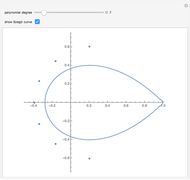
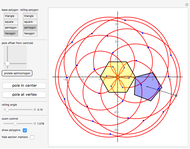
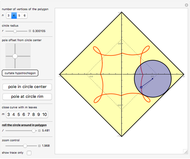
Let be the coefficients of a Fourier expansion of a regular polygon with 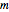sides. This Demonstration plots the partial sums of the Fourier series 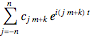as they converge to -gons. The vertices remain slightly rounded as a result of the Gibbs phenomenon.

[more]

A regular self-intersecting star polygon is created by connecting one vertex of a regular -sided polygon to a nonadjacent vertex and continuing until the path returns to the original vertex; this process would need to be repeated if , but such pairs are avoided here.

[less]

Contributed by: Izidor Hafner (January 2016)
Based on work by: Frank F. Farris
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] F. A. Farris, Creating Symmetry, The Artful Mathematics of Wallpaper Patterns, Princeton: Princeton University Press, 2015 p. 30.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send