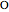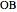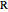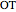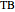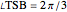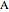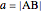Pappus's Hexagons

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
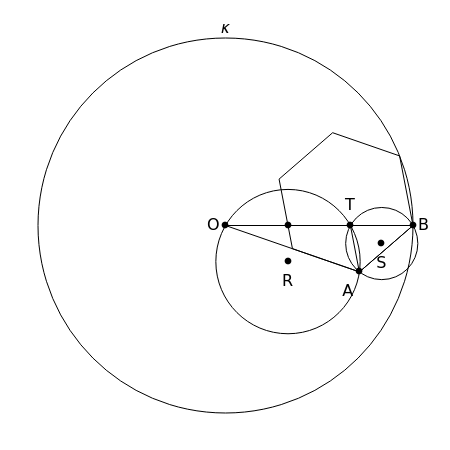
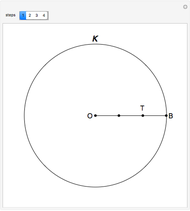
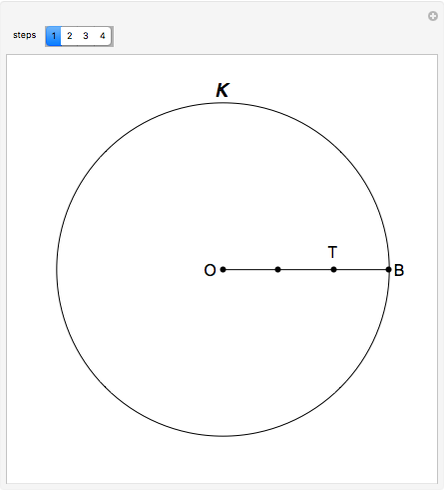
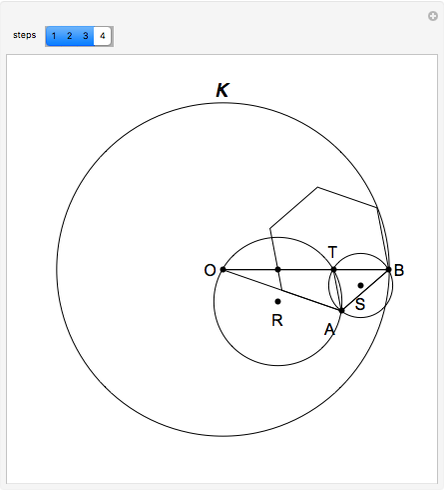
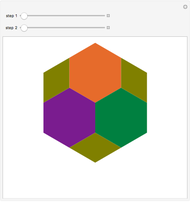
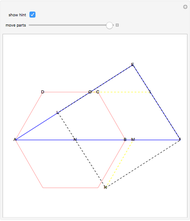
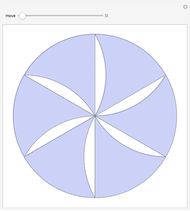
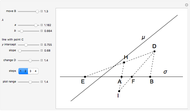
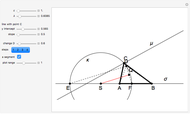
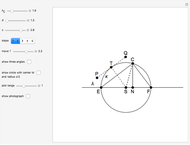
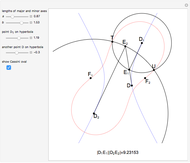
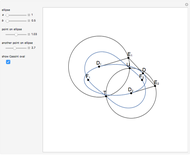
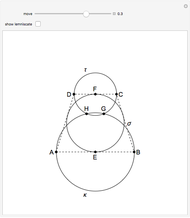
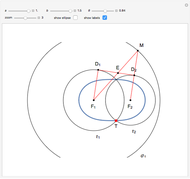
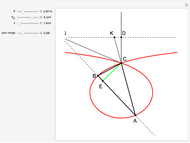
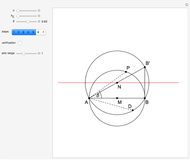
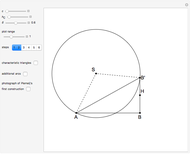
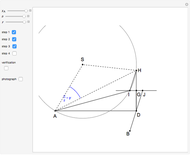
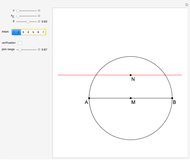
This following construction problem was solved by Pappus. Given a circle, inscribe in it seven congruent regular hexagons, such that one is is centered at the center of the circle, the other six each have one side in common with it, and their opposite sides are chords of the circle.
[more]
Contributed by: Marko Razpet and Izidor Hafner (June 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
What is the connection between  and
and  ? By the law of cosines,
? By the law of cosines, 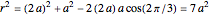 .
.
References
[1] T. Heath, A History of Greek Mathematics, Volume II: From Aristarchus to Diophantus, New York: Dover Publications, 1981.
[2]. A. Ostermann and G. Wanner, Geometry by Its History, New York: Springer, 2012.
Permanent Citation