Gauss-Bonnet and Poincaré-Hopf for Graphs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
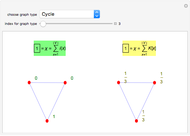
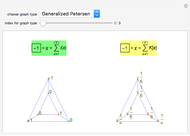
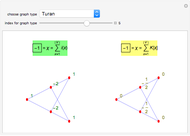
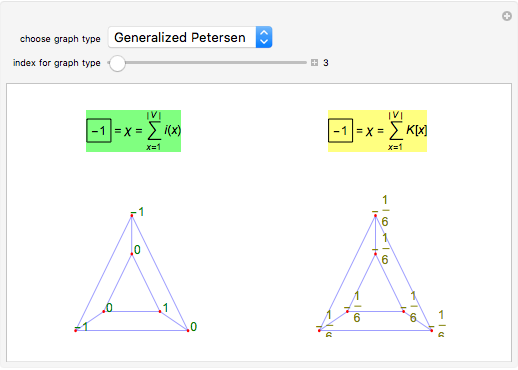
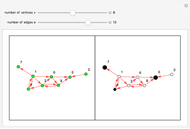
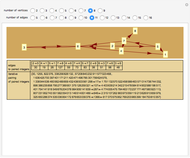
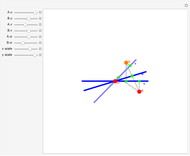
Two representations of a selected graph are shown. On the left, the vertices are labeled with the indices, which add up to the Euler characteristic of the graph. On the right, the graph is shown with curvatures, which also sum to the Euler characteristic. The left graphic illustrates a Gauss–Bonnet theorem for graphs. The right graphic illustrates a Poincaré–Hopf theorem for graphs.
Contributed by: Oliver Knill (January 2012)
(Harvard University)
Open content licensed under CC BY-NC-SA
Details
The Gauss–Bonnet theorem for graphs is covered in [1] and [2]. The statistics about curvature and dimension are covered in [3], where explicit formulas for the average dimension and Euler characteristic of Erdos–Renyi probability spaces can be found. [4] proves a Poincaré–Hopf theorem for graphs.
The main ingredients are local quantities curvature 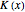 and index
and index  , where
, where  denotes the Euler characteristic of a graph and
denotes the Euler characteristic of a graph and 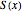 is the part of the unit sphere where
is the part of the unit sphere where 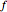 is smaller than
is smaller than  .
.
The sum of all the curvatures is the Euler characteristic: This is a Gauss–Bonnet–Chern theorem; see [2], which also explores it in a more geometric setting. The sum of all the indices is the Euler characteristic. This is a discrete version of a Poincaré–Hopf theorem [4]. References
[1] O. Knill. "A Discrete Gauss–Bonnet Type Theorem." arXiv. (Sep 13, 2010) arxiv.org/abs/1009.2292.
[2] O. Knill. "A Graph Theoretical Gauss–Bonnet–Chern Theorem." arXiv. (Nov 23, 2011) arxiv.org/abs/1111.5395.
[3] O. Knill. "On the Dimension and Euler Characteristic of Random Graphs." arXiv. (Dec 24, 2011) arxiv.org/abs/1112.5749.
[4] O. Knill. "A Graph Theoretical Poincare–Hopf Theorem." arXiv. (Jan 5, 2012) arxiv.org/abs/1201.1162.
Snapshots
Permanent Citation