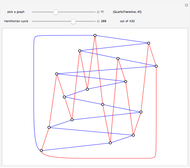
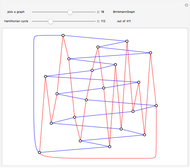
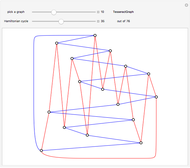
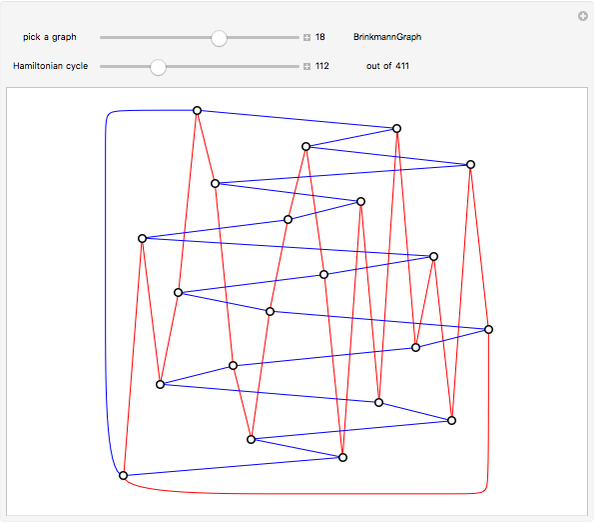
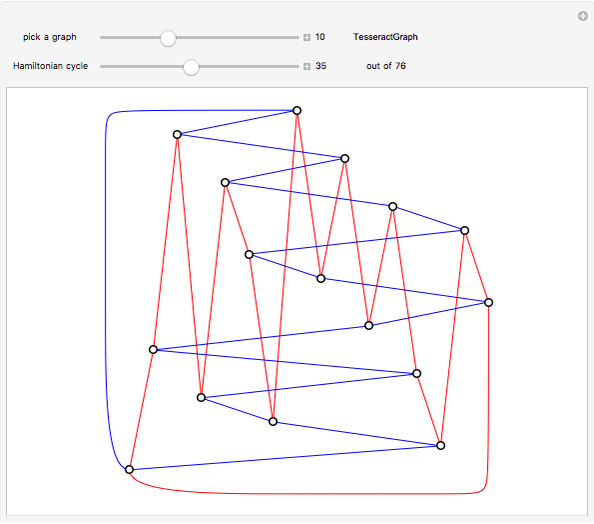
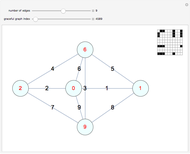
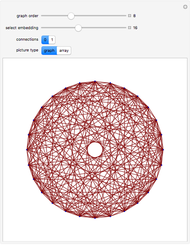
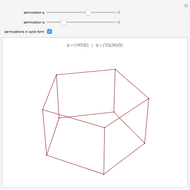
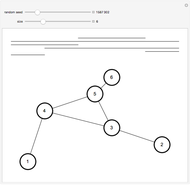
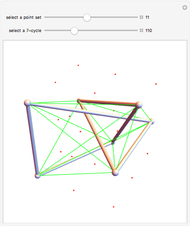
If the edges of a graph can be partitioned into two planar graphs, it has thickness 2 (a biplanar graph). This Demonstration shows some thickness-2 embeddings of various quartic graphs. In the first step a Hamiltonian cycle is chosen. One of the graphs, the icosidodecahedral graph (26), is planar and actually has thickness 1.