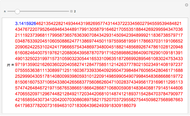
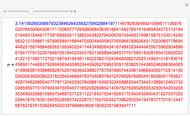
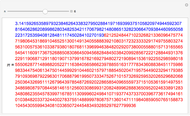
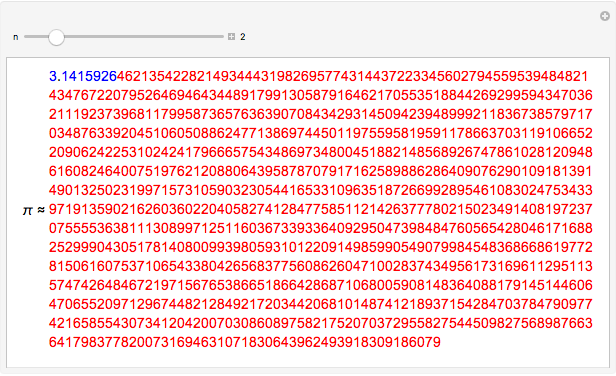
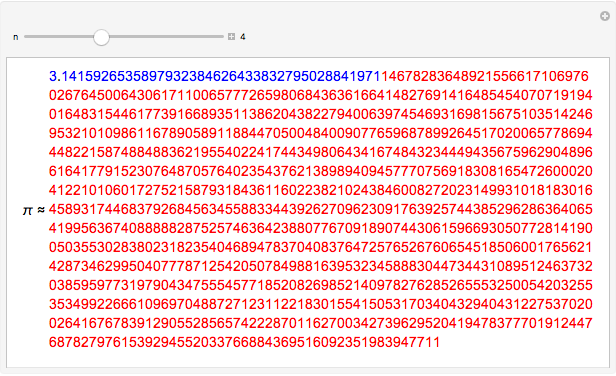
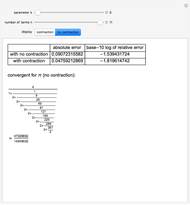
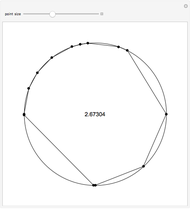
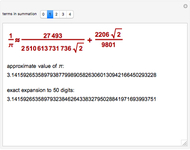
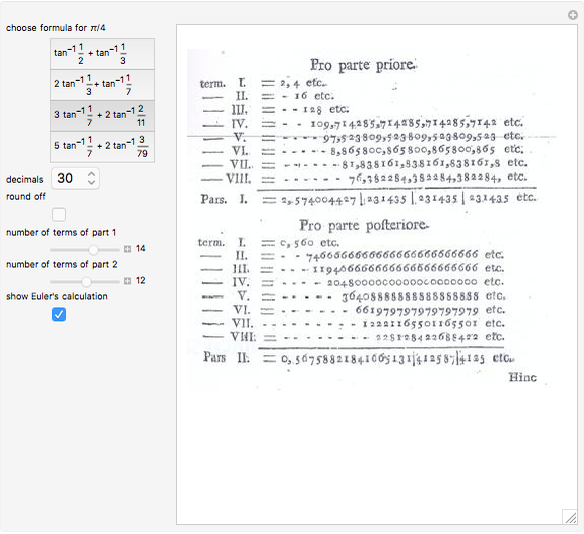
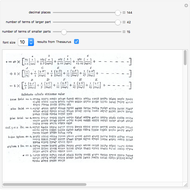
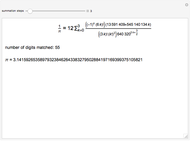
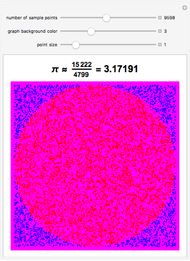
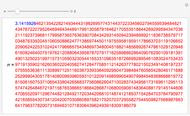
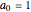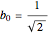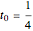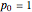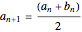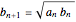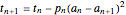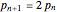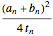3.140579250522168248311331268975823311773440237512948335643486693345 |
58275803490290782728762155276690054600542214681392392660377113165273 |
94502599282021373726674237102334610829243413150727872688025465644705 |
28512459515402613483972677323877167912273242684048203139002537509117 |
74467749677985970852941659103369862038800169128364541067528504295037 |
18532198839982181412863912905298516564960825702694249040704828539096 |
48264677804949679280099521464982038521971842843043042034578372562498 |
68007082232022603619332117823848276684858446989052198390833065071290 |
92351606755194654144624135390024548136188099823075099649772860945401 |
70736736697016545900073228958450923617293812909309146676189725112647 |
59177370867567839915469417008512430870172293262787616014502438293686 |
09583032322610999584843630113675736291388919050863279488715078501658 |
67051418045724650344117517479054769631536442522283224388018096944998 |
41555152459422196489123477377147477676852879826617970116776367738677 |
2878322823597320158075037952904881463664550414203 |

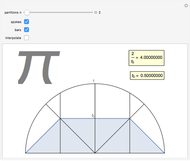
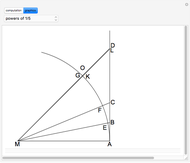
 . With the initial values
. With the initial values