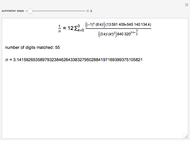
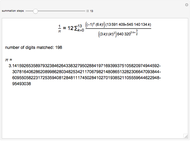
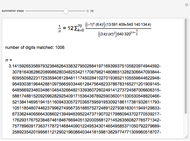
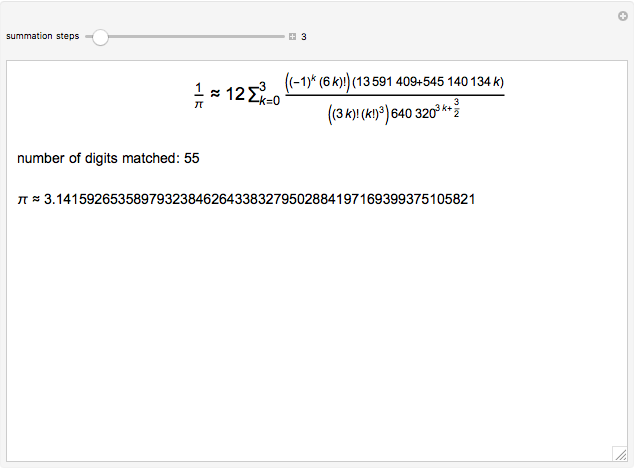
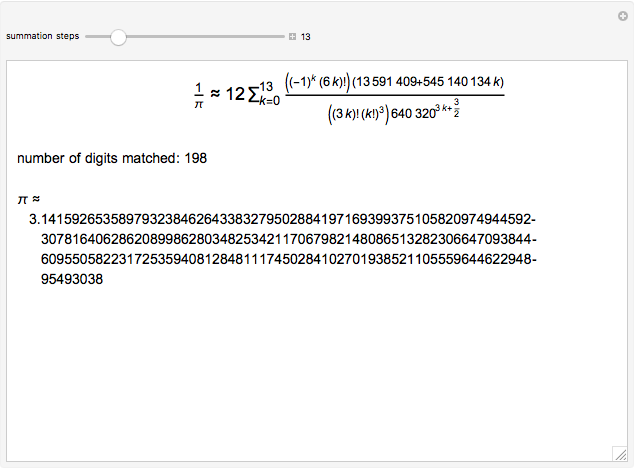
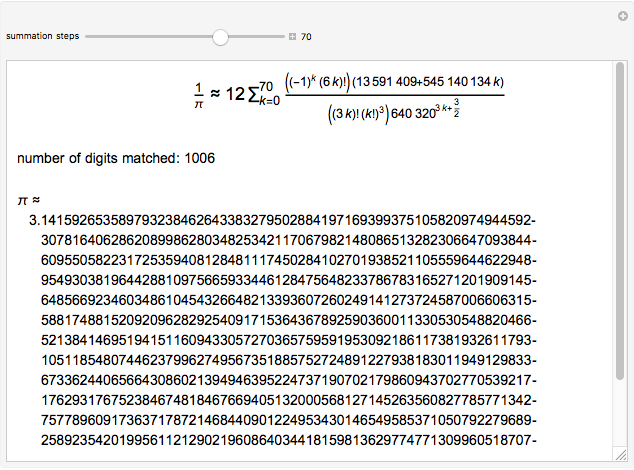
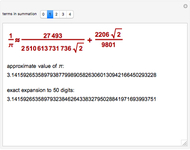
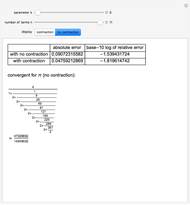
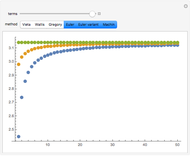
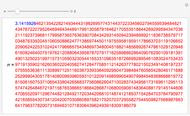
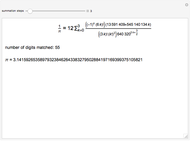
The Chudnovsky algorithm generates 14 or more digits of for every summation step. It has been used to achieve numerous world record calculations for since it was published in 1989. As implemented here, Mathematica calculates an approximation to for a number of summation steps that you set. The Demonstration shows how many total digits of have been correctly computed as a result.