Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Wagon Wheel Approximation of Pi

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

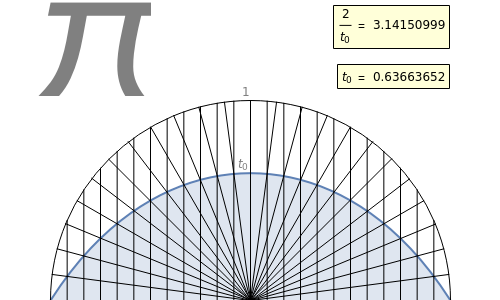
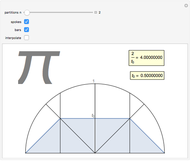
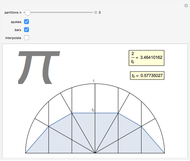
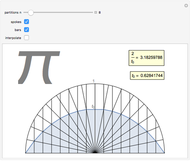
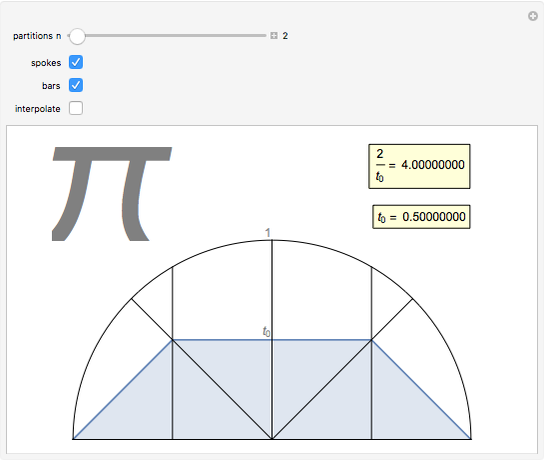
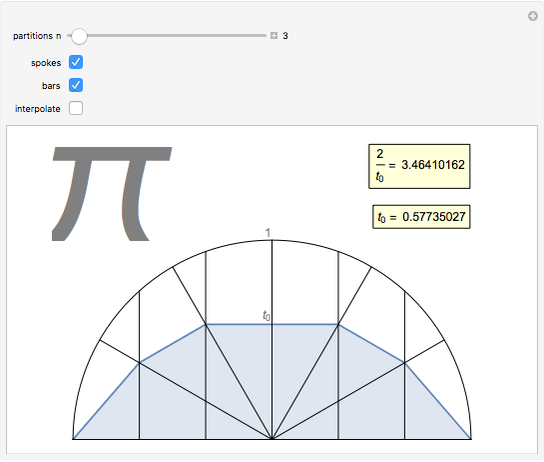
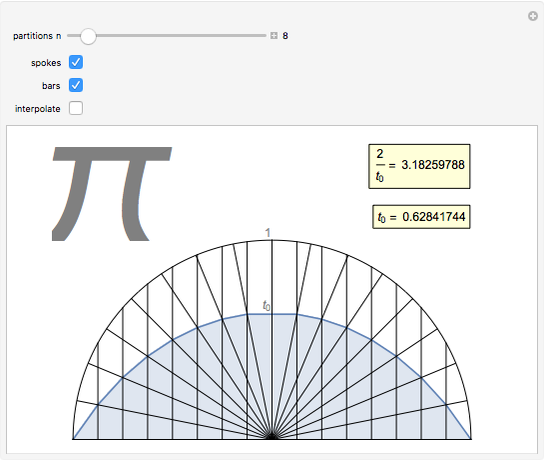
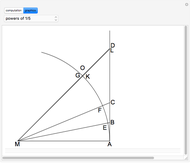
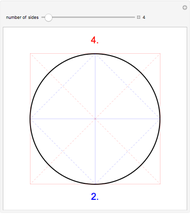
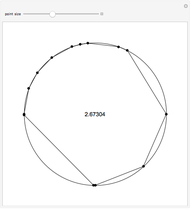
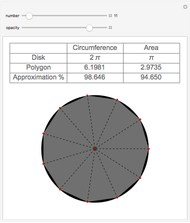
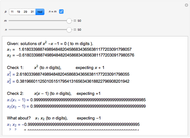
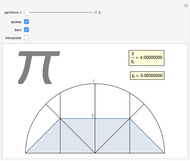
Let there be spokes of a wagon wheel. We only need to deal with the upper half of a unit circle. Divide the semicircle vertically into evenly spaced segments using bars.

[more]

The intersections of the spokes with the corresponding vertical bars creates truncated spokes of length , , rather than of length 1. Here and .

Notice that is undefined by an intersection because both the spoke and bar are vertical and coincide. The value of must be inferred from the pattern created by connecting the intersections—amazingly, approaches as increases!

[less]

Contributed by: Robert L. Brown (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

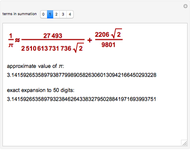
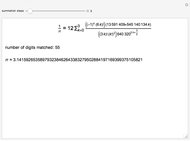
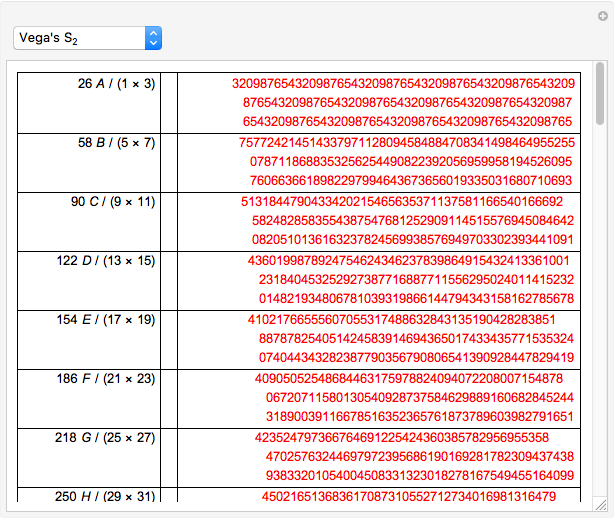
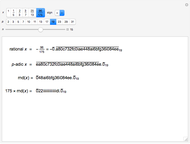
This Demonstration leads to one of the many beautiful expressions for :

,

(from the French mathematician Viète, 1593).

This formula comes from the cosine half-angle formula, which yields

,

,

, and so on.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send