Geometry of Quartic Polynomials

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
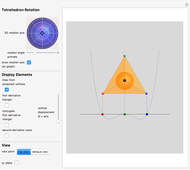
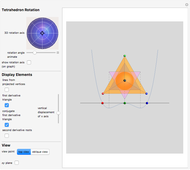
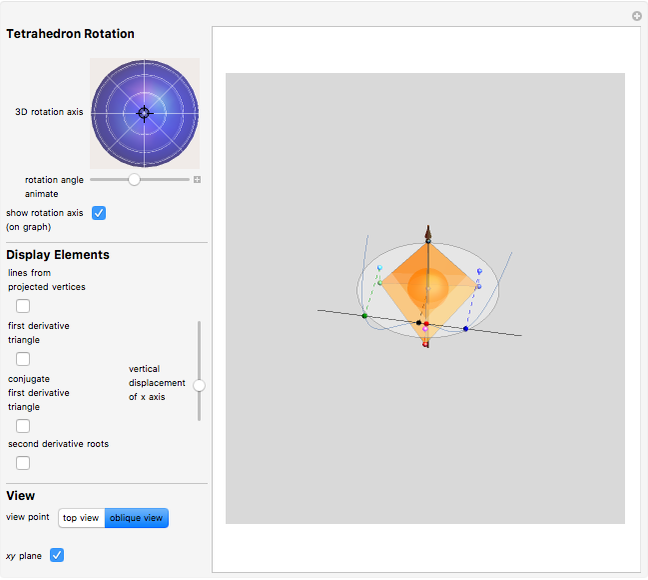
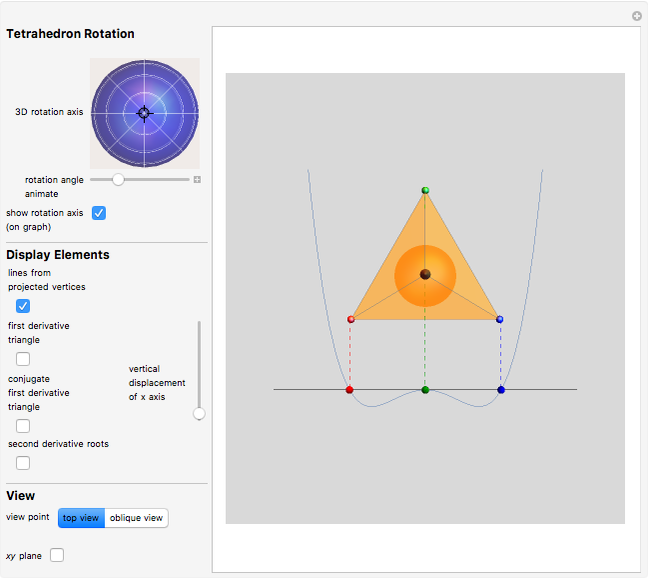
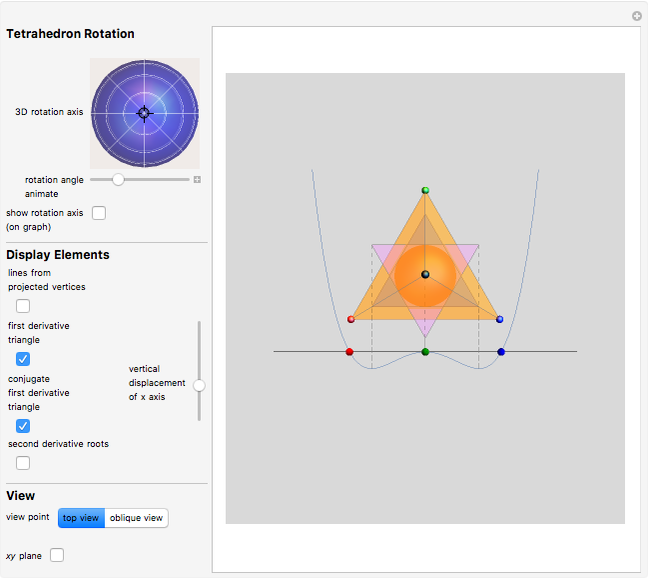
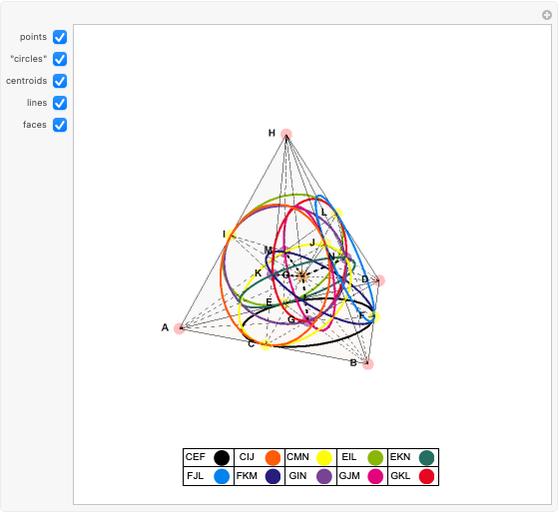
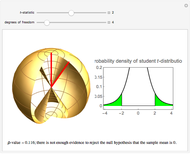
Given a quartic 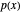 with four real roots (at least two distinct), those roots are the first coordinate projections of a regular tetrahedron in
with four real roots (at least two distinct), those roots are the first coordinate projections of a regular tetrahedron in 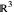 . That tetrahedron has a unique inscribed sphere, which projects onto an interval whose endpoints are the two roots of
. That tetrahedron has a unique inscribed sphere, which projects onto an interval whose endpoints are the two roots of 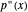 . Let
. Let  ,
, ,
,  be the roots of
be the roots of 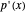 ; then the points
; then the points 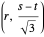 ,
, 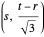 ,
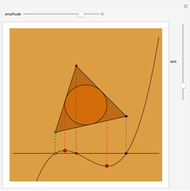
, 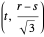 form an equilateral triangle whose vertices project on the critical points of the quartic
form an equilateral triangle whose vertices project on the critical points of the quartic  (this is the "first derivative triangle"). A similar triangle is formed by negating the
(this is the "first derivative triangle"). A similar triangle is formed by negating the 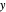 coordinates of these points ("conjugate first derivative triangle"). This application is relevant to the following so far open conjecture: there does not exist a quartic polynomial
coordinates of these points ("conjugate first derivative triangle"). This application is relevant to the following so far open conjecture: there does not exist a quartic polynomial 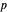 with four distinct rational roots such that
with four distinct rational roots such that  ,
, 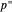 , and
, and 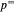 all have rational roots.
all have rational roots.
Contributed by: Salvador Jesús Gutiérrez Martínez (April 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
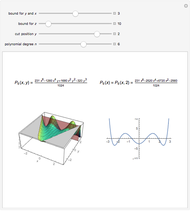
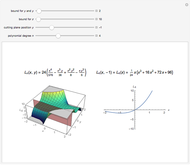
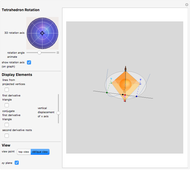
Tetrahedron rotation: to rotate the tetrahedron independently of the polynomial, choose a rotation axis with the trackball and an angle with the slider.
Snapshot 1: tetrahedron vertices are projected on the 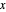 -
-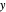 p
p lane
lane
Reference
[1] S. Northshield, "Geometry of Cubic Polynomials," Mathematics Magazine, 86, 2013 pp. 136–143.
[2] R. W. D. Nickalls, "The Quartic Equation: Alignement with an Equivalent Tetrahedron," The Mathematical Gazette, 96(535), 2012 pp. 49–55.
Permanent Citation