Mathematica MathWorld Wolfram Science More »

Ikeda Delay Differential Equation


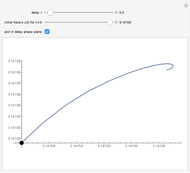
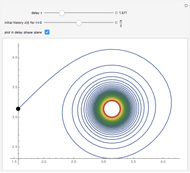
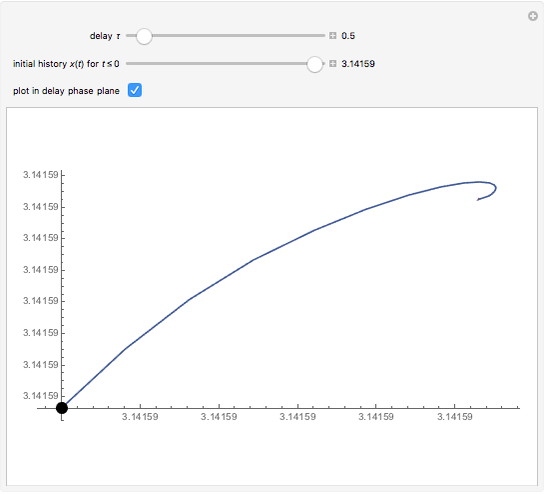
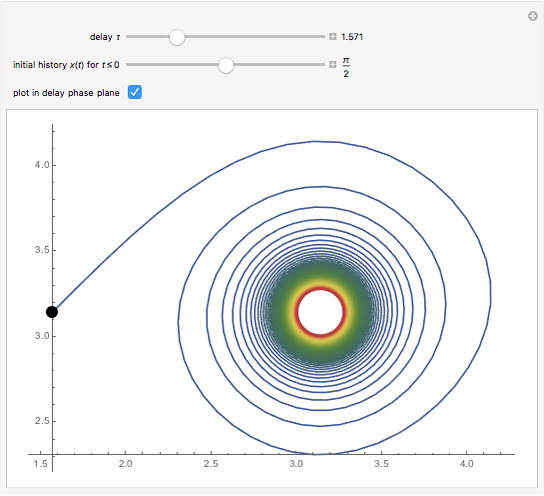
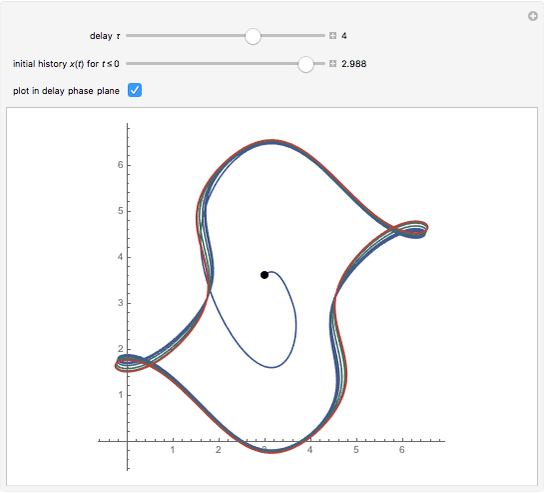
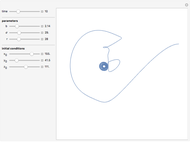
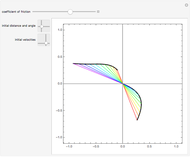
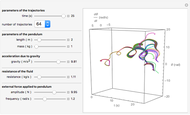
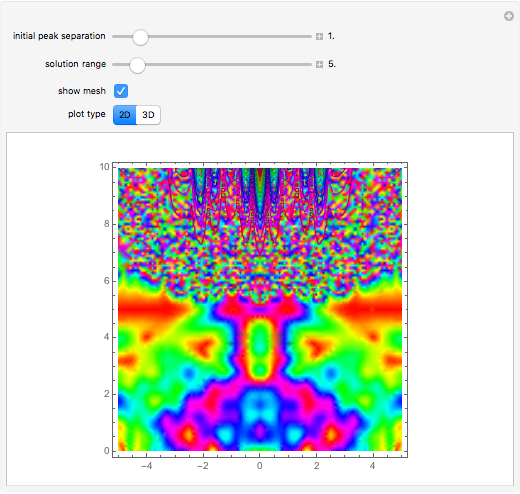
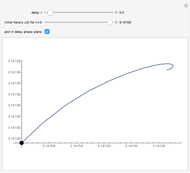
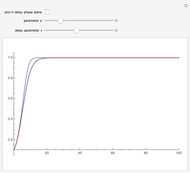
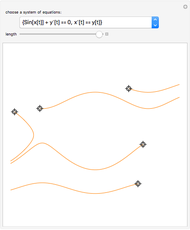
	This Demonstration shows solutions of the Ikeda delay differential equation, 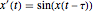, a very simple equation with complex chaotic dynamics.


	Contributed by: Rob Knapp

A form of the equation was first proposed to model an optical bistable resonator system [1]. The route to chaos as

increases to

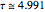is described in [2]. For larger values of

the solutions look and behave statistically like Brownian motion.

Snapshot 1: just above the value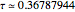

, where the stable quilibrium changes from a node to a focus

Snapshot 2: just above the value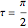

, at which there is a Hopf bifurcation and the appearance of a limit cycle

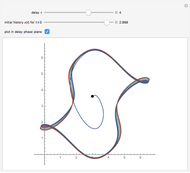
Snapshot 3: just above the value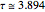

, at which a pitchfork bifurcation occurs, leading to two coexisting limit cycles

Snapshot 4: the other limit cycle for the same value of

; the initial condition is very close to that of snapshot 3

Snapshot 5: just above the value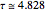

, at which a period doubling occurs

Snapshot 6: just above the value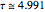

, where chaos first occurs; note how the solution looks much like Brownian motion

Snapshot 7: just above the value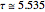

where a periodic window appears

[1] K. Ikeda and K. Matsumoto, "High-Dimensional Chaotic Behavior in Systems with Time-Delayed Feedback," Physica D, 29, 1987 p. 223.

[2] J. C. Sprott, "A Simple Chaotic Delay Differential Equation," Physics Letters A, 366, 2007 pp. 397–402.

Contributed by: Rob Knapp

Report an issue »

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

RSS

Atom