Delay Logistic Equation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
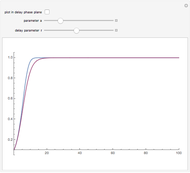
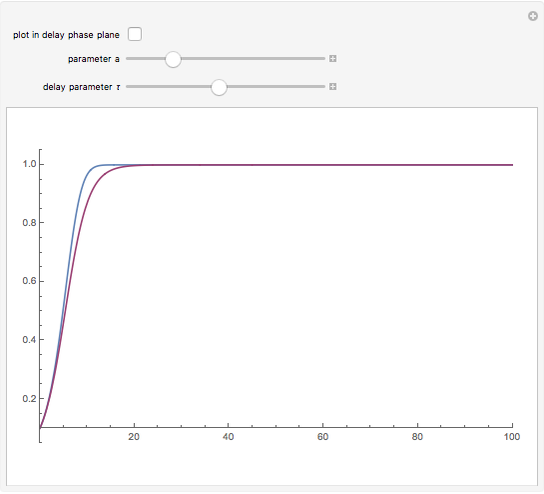
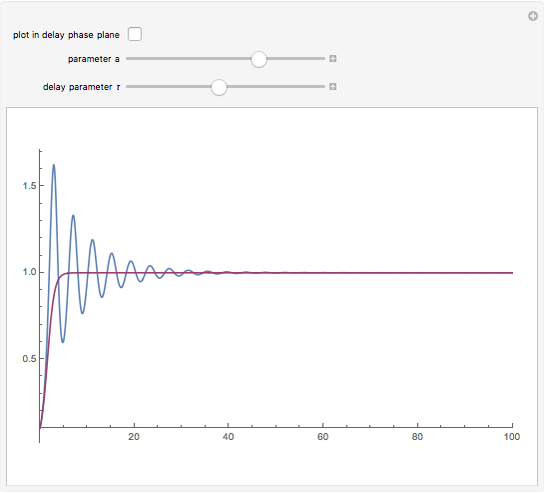
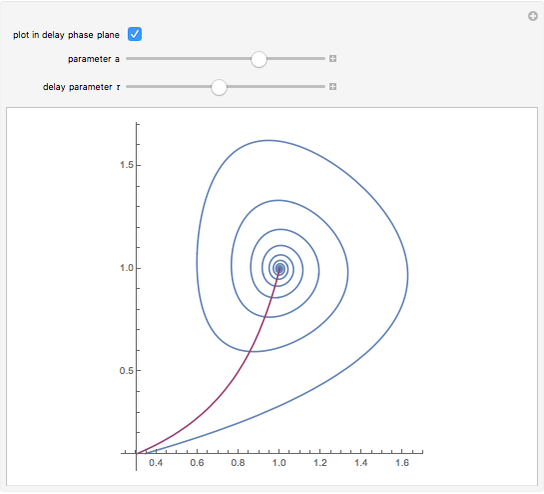
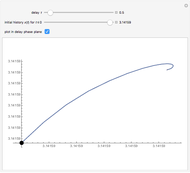
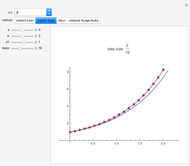
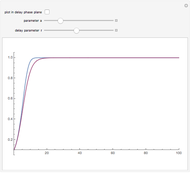
This shows the solution of the scalar delay logistic equation  in blue along with the solution of the logistic equation without delay (
in blue along with the solution of the logistic equation without delay ( ) in red.
) in red.
Contributed by: Rob Knapp (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For  , solutions are monotonic. For
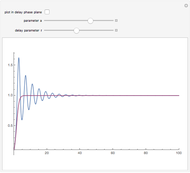
, solutions are monotonic. For  , the solutions are oscillatory and asymptotically approach
, the solutions are oscillatory and asymptotically approach  . For
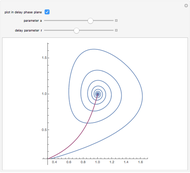
. For  , the solutions approach a limit cycle. The boundaries can be determined by considering the test solution
, the solutions approach a limit cycle. The boundaries can be determined by considering the test solution  , which gives the equation
, which gives the equation  ; that has the solution
; that has the solution  , where
, where  is the ProductLog function.
is the ProductLog function.
Reference: K. Gopalsamy, Stability and Oscillations in Delay Differential Equations of Population Dynamics, Boston: Kluwer, 1992.
Permanent Citation