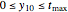Visualizing the Solution of Two Linear Differential Equations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
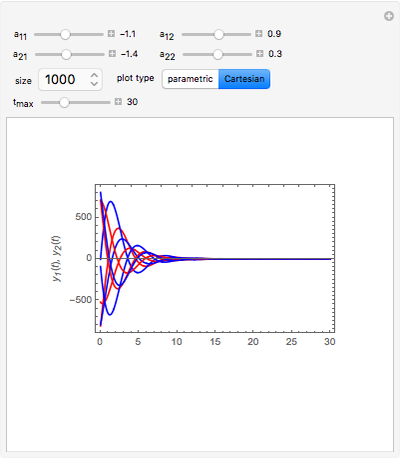
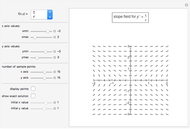
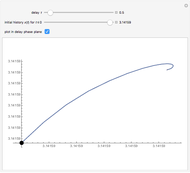
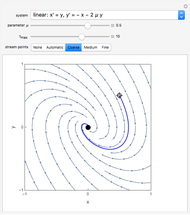
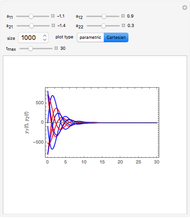
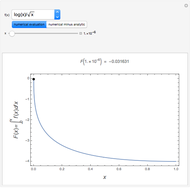
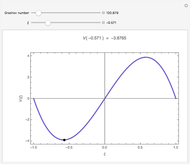
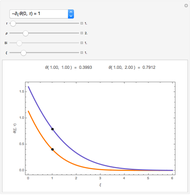
The analytical solutions of the two differential equations  and
and 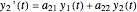 , subject to the initial conditions
, subject to the initial conditions  and
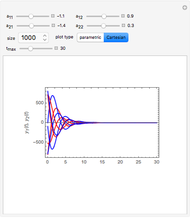
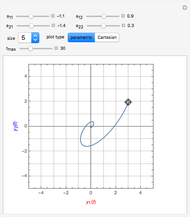
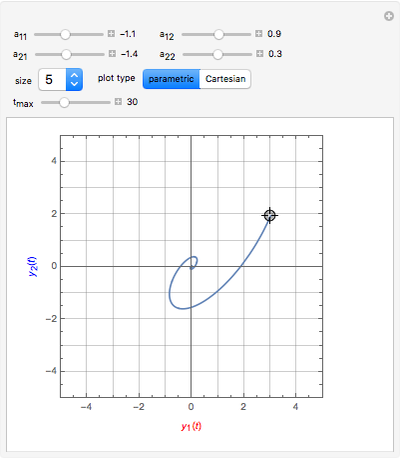
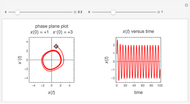
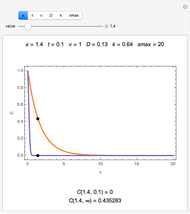
and 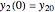 are used to create two plots, a parametric plot of a curve with horizontal coordinate
are used to create two plots, a parametric plot of a curve with horizontal coordinate 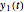 and vertical coordinate
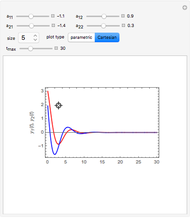
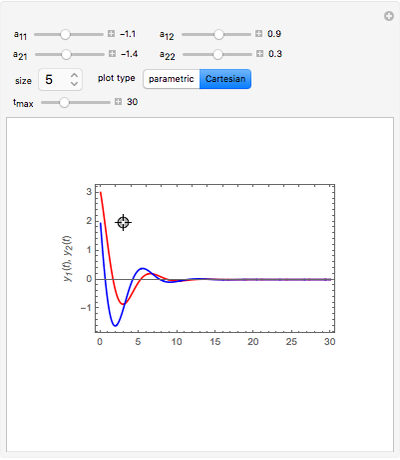
and vertical coordinate  and a standard plot of
and a standard plot of 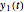 and
and  as functions of
as functions of  from 0 to
from 0 to  .
.
Contributed by: Mikhail Dimitrov Mikhailov (March 2011)
Open content licensed under CC BY-NC-SA
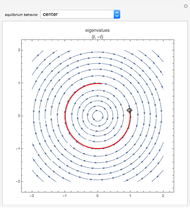
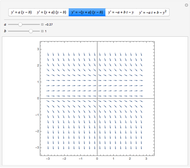
Snapshots
Details
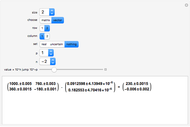
The expressions for 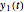 and
and  given by the Mathematica built-in function DSolve are not applicable when
given by the Mathematica built-in function DSolve are not applicable when 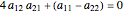 . For this special case the solutions are simplified using Mathematica's Limit function. Thus our function twoDSolve correctly computes
. For this special case the solutions are simplified using Mathematica's Limit function. Thus our function twoDSolve correctly computes 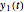 and
and  for all parameters specified.
for all parameters specified.
Permanent Citation