Illustrating the Law of Large Numbers

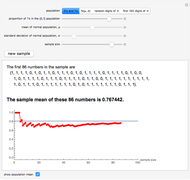
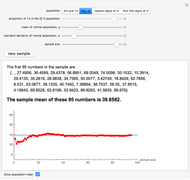
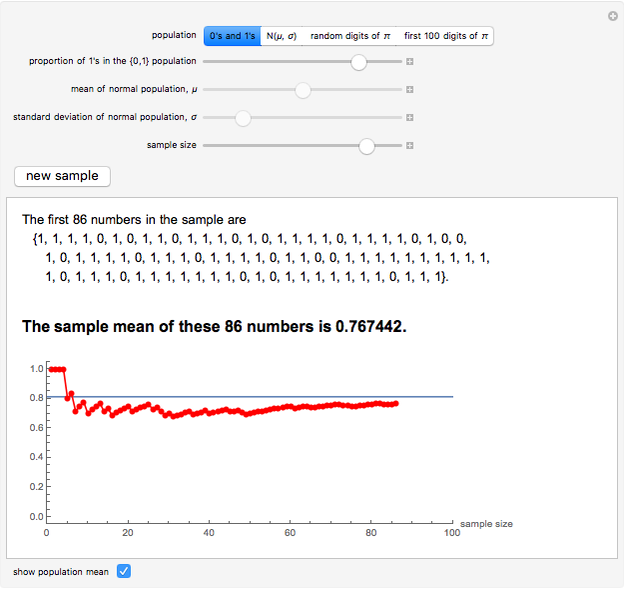
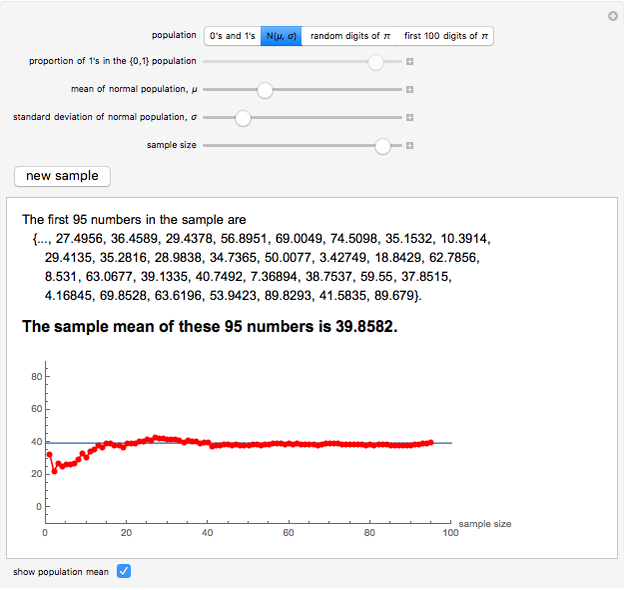
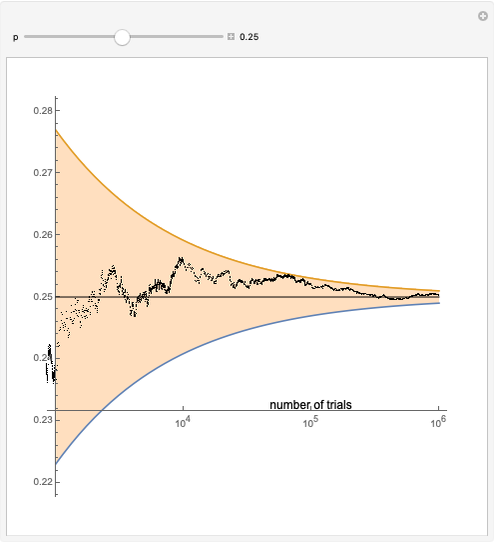
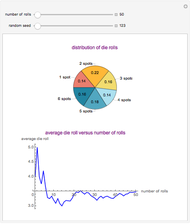
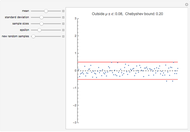
The law of large numbers states (informally) that as the number of independent observations drawn from a population with finite mean increases, the mean of those observed values approaches . This Demonstration illustrates that behavior by plotting the sample mean as a function of the current sample size , for to . 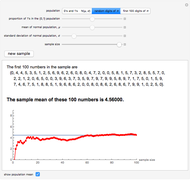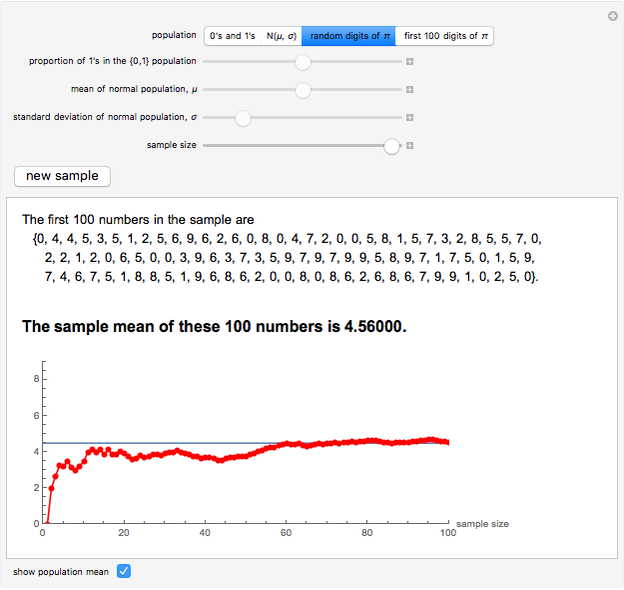Random samples can be drawn from a population of 0's and 1's (with any proportion of 1's), a normal population (with a range of and available), or from the (first 100,000) digits of . The first 100 digits of are available as a population, with samples of size consisting of the first digits, to allow for classroom illustration with a familiar and frequently referred to as random set of digits.