Law of Large Numbers: Dice Rolling Example

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
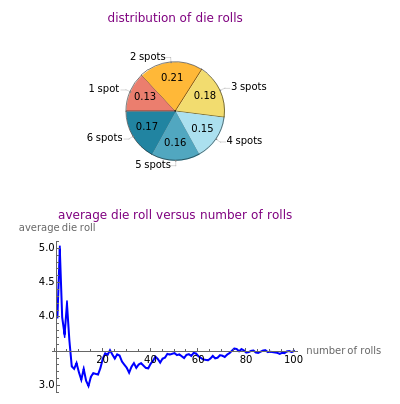
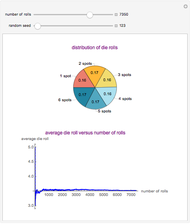
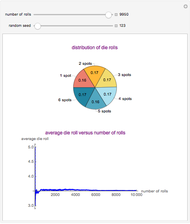
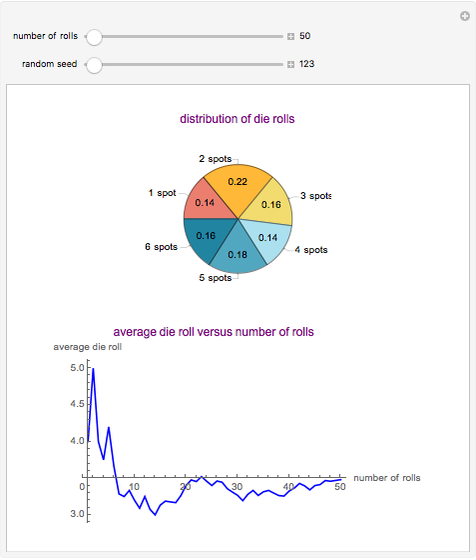
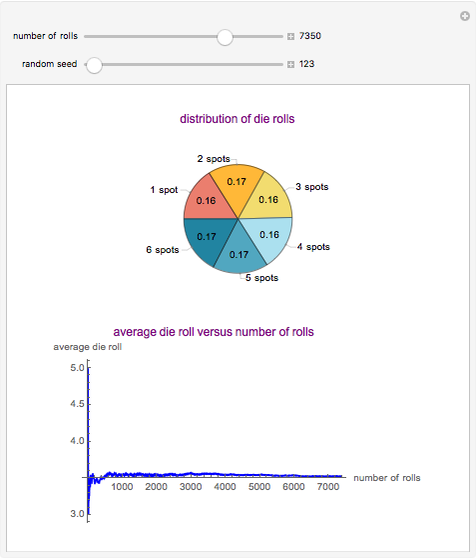
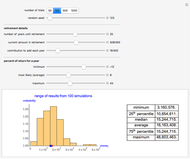
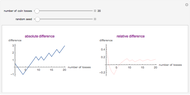
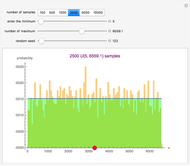
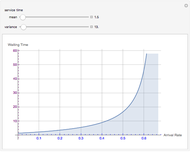
This Demonstration showcases the law of large numbers, a key theorem in probability theory, which describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value, and will tend to become closer as more trials are performed. For this Demonstration, consider rolling a die  times. If each roll is independent of the next (the result of one roll does not change the probabilities of any number of spots appearing), then the average of the rolls should converge to 3.5 (expected value for the roll of a die) as
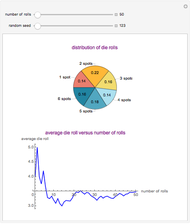
times. If each roll is independent of the next (the result of one roll does not change the probabilities of any number of spots appearing), then the average of the rolls should converge to 3.5 (expected value for the roll of a die) as  gets large. This Demonstration simulates a user-defined number of rolls of the die. The pie chart shows the distribution of the number of spots that appear and the bottom plot shows the average number of die rolls. As the number of rolls increases, the average will converge to 3.5.
gets large. This Demonstration simulates a user-defined number of rolls of the die. The pie chart shows the distribution of the number of spots that appear and the bottom plot shows the average number of die rolls. As the number of rolls increases, the average will converge to 3.5.
Contributed by: Paul Savory (University of Nebraska-Lincoln) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Law of Large Numbers: Dice Rolling Example"
http://demonstrations.wolfram.com/LawOfLargeNumbersDiceRollingExample/
Wolfram Demonstrations Project
Published: March 7 2011