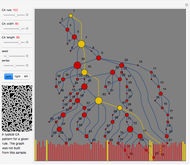
Is This Graph Planar?

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
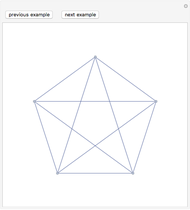
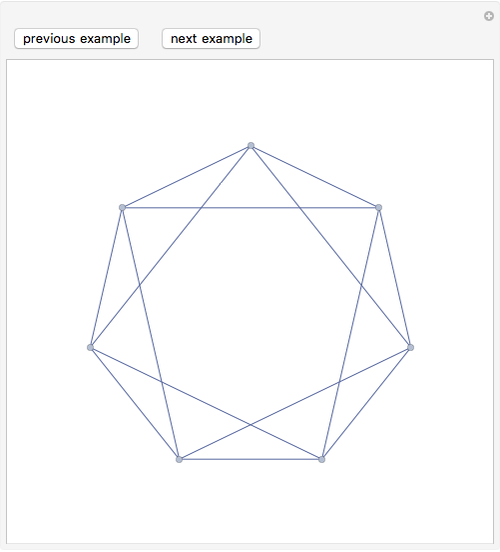
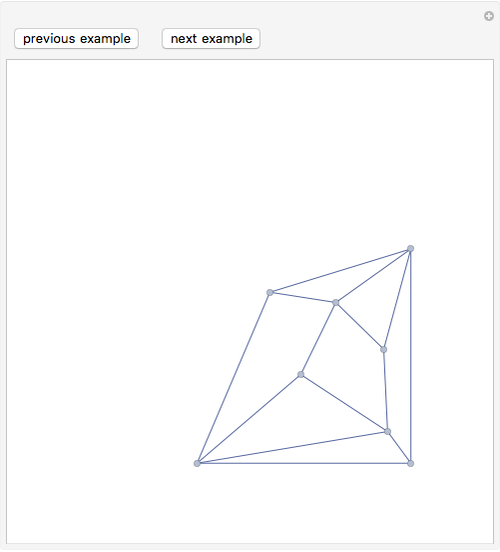
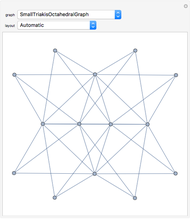
A graph  is planar if it can be drawn in the plane in such a way that no two edges meet except at a vertex with which they are both incident. Any such drawing is a plane drawing of
is planar if it can be drawn in the plane in such a way that no two edges meet except at a vertex with which they are both incident. Any such drawing is a plane drawing of 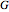 . A graph is nonplanar if no plane drawing of
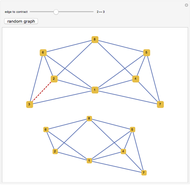
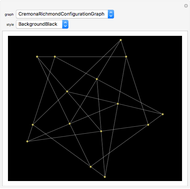
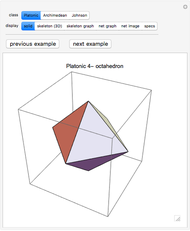
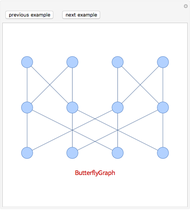
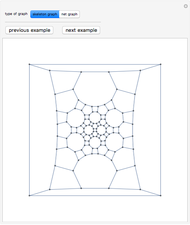
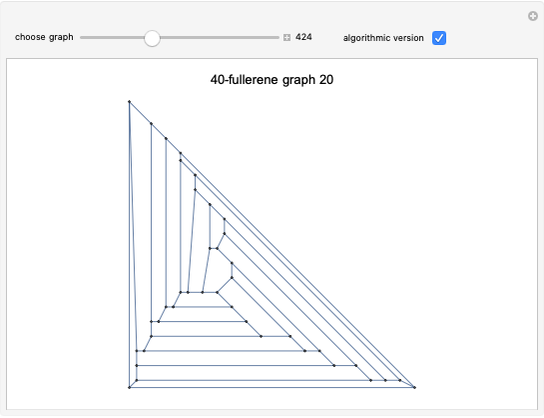
. A graph is nonplanar if no plane drawing of 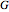 exists. Trees, path graphs, and graphs having less than five vertices are planar. Although since as early as 1930 a criterion for a graph to be planar was known (Kuratowski's theorem), it turned out to be difficult to use. In this Demonstration we have chosen a selection of graphs for you to test for planarity. They form a small selection of the many available in Mathematica 8. By dragging the vertices, either conjecture that it is nonplanar or try to unravel a chosen graph to get a planar drawing (if a graph is planar, this procedure will be successful, as any planar graph has a drawing in which every edge is represented by a straight line). The purpose of this Demonstration is to give you an intuitive feeling for the complexity behind a method to automatically test for planarity.
exists. Trees, path graphs, and graphs having less than five vertices are planar. Although since as early as 1930 a criterion for a graph to be planar was known (Kuratowski's theorem), it turned out to be difficult to use. In this Demonstration we have chosen a selection of graphs for you to test for planarity. They form a small selection of the many available in Mathematica 8. By dragging the vertices, either conjecture that it is nonplanar or try to unravel a chosen graph to get a planar drawing (if a graph is planar, this procedure will be successful, as any planar graph has a drawing in which every edge is represented by a straight line). The purpose of this Demonstration is to give you an intuitive feeling for the complexity behind a method to automatically test for planarity.
Contributed by: Jaime Rangel-Mondragon (November 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Is This Graph Planar?"
http://demonstrations.wolfram.com/IsThisGraphPlanar/
Wolfram Demonstrations Project
Published: November 2 2011