Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Longitudinal Oscillations and Resonance of a Four-Spring, Three-Mass System

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

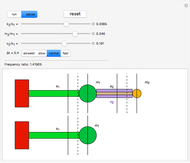
Study the longitudinal oscillations and forced vibrations of this system with three degrees of freedom. You can set the initial conditions and the spring strength, damping coefficients, etc.

[more]

You can view the free vibrations by setting the frequency of the exciting force to 0. By setting the frequency to one of the resonance frequency values displayed, you can see that resonance. There are three different resonance frequencies, corresponding to the different oscillation modes.

The slider changes the elongation of the first mass (masses are the red dots), which is the leftmost one. The is for the second, which is the middle one, and is for the rightmost mass.

All three bodies have the same mass and they can be changed with the first slider.

The external force "shakes" the right end of the fourth spring with a constant frequency, while the left end of the first spring is fixed.

This frequency can be set with the third slider.

If this frequency is set to 0 then the system performs free vibrations.

The units of the longitudinal elongations are meters.

[less]

Contributed by: Árpád Kósa (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

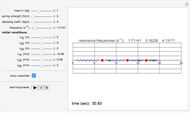
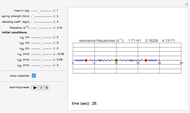
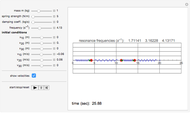
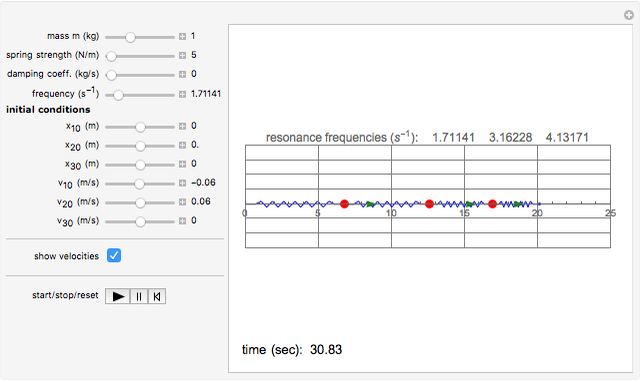
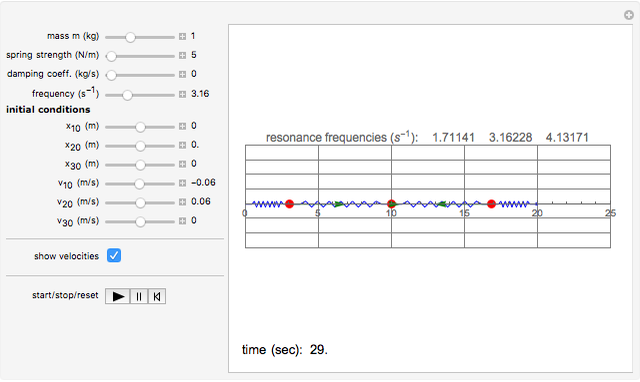
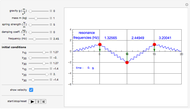
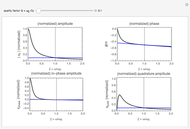
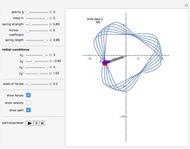
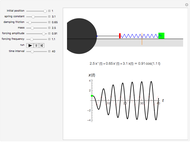
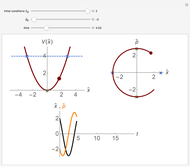
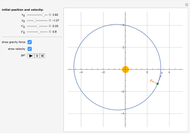
This is a simple mechanical system with four identical springs and three bodies of equal mass. Only longitudinal oscillations are allowed. This system has three different frequencies at which resonance occurs; these frequency values are displayed. If you set the frequency of the exciting force to one of the resonance values and set the damping coefficient to 0, you can see the strong oscillations characteristic of the resonance phenomenon.

You can observe the three different oscillation modes at the different resonance frequencies. These resonance frequencies are the so-called eigenvalues of the functions describing the oscillations of this system.

The exciting force acts on the right side of the spring chain.

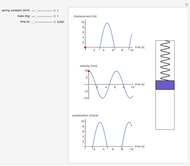
For free vibrations, set the exciting force frequency to 0. In this case you can set the positions and initial velocities and then see the free oscillations.

For a much more detailed description, see L. D. Landau and E. Lifshitz, Course of Theoretical Physics, Vol. 1, Oxford: Pergamon Press, 1960.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send