Anharmonic Oscillator Phase Space Trajectories 2D

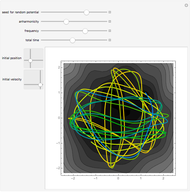
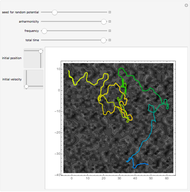
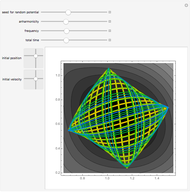
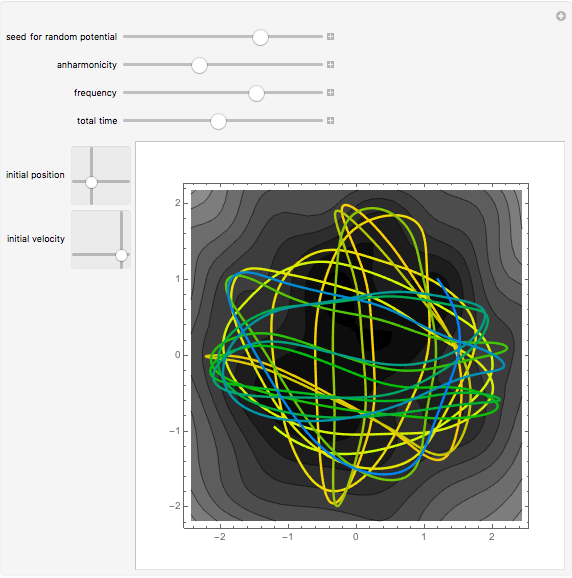
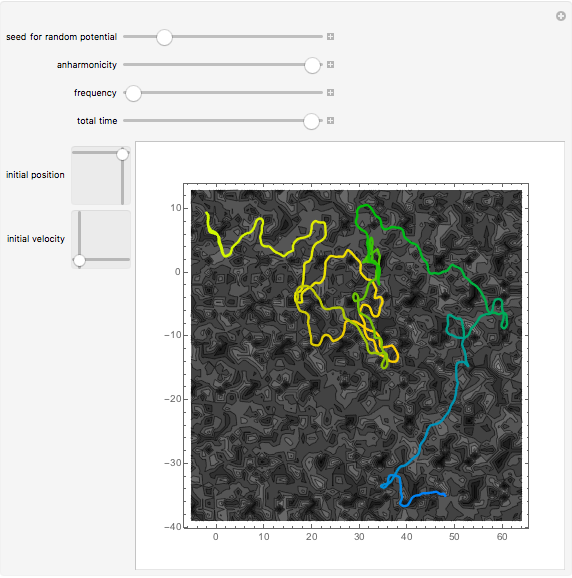
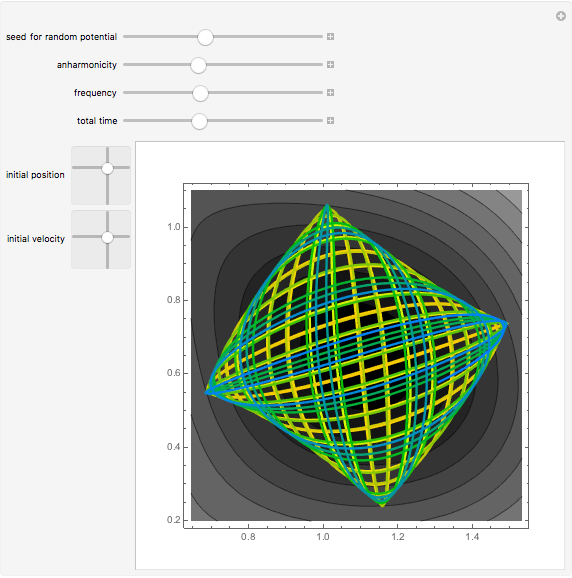
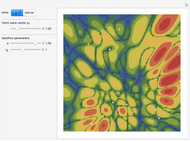
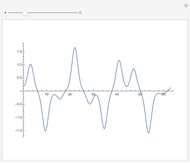
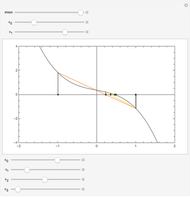
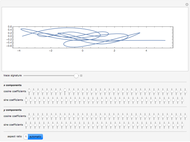
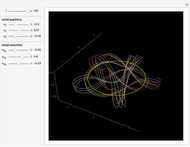
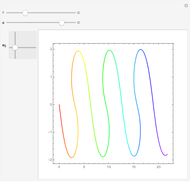
Independent of the initial conditions, the trajectories in a 2D harmonic oscillator are ellipses. Adding an anharmonic contribution to the potential generally changes the form of the trajectories (obtained by solving Newton's equations of motion), into nonperiodic, complicated curves. This demonstrates trajectories of an anharmonic 2D oscillator plotted over a contour plot of the potential.