Synchronization of Coupled Phase Oscillators

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
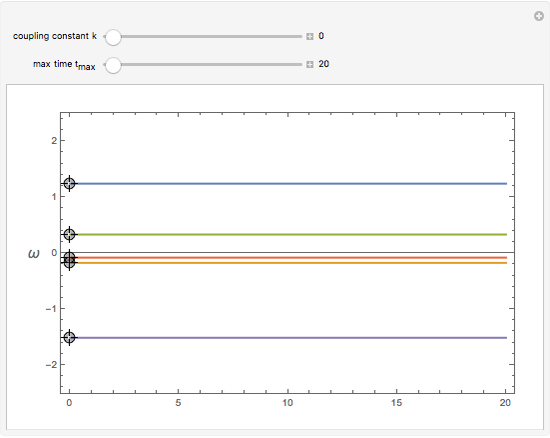
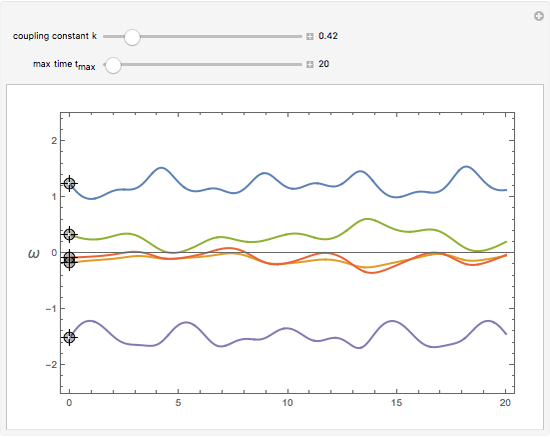
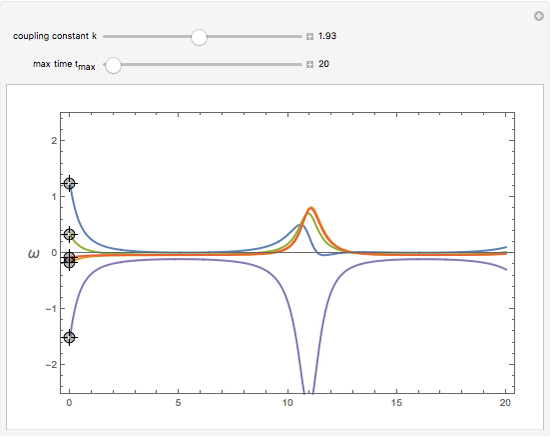
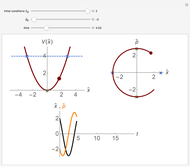
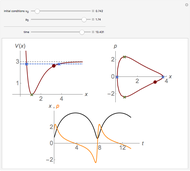
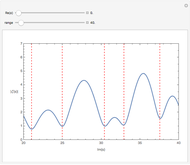
In 1665, Huygens discovered that two pendula suspended side-by-side eventually synchronize. Today it is known that synchronization is a common feature of interacting oscillatory systems. This Demonstration visualizes the synchronization of coupled phase oscillators. The plot shows the time variation of the oscillator frequencies. When the coupling constant is 0, there is no interaction between the oscillators, so each oscillator has a different frequency. As the coupling constant increases, you can observe synchronization. It turns out that the synchronization frequency is the average of the initial frequencies.
Contributed by: Baris Altunkaynak (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The equations of motion are given by the coupled differential equations:
 ,
,
where 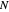 is the number of oscillators,
is the number of oscillators,  is the coupling constant, and
is the coupling constant, and 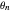 is the phase of the
is the phase of the 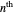
 oscillator.
oscillator.
Permanent Citation