Macaulay Duration as the Balancing Point of a Seesaw

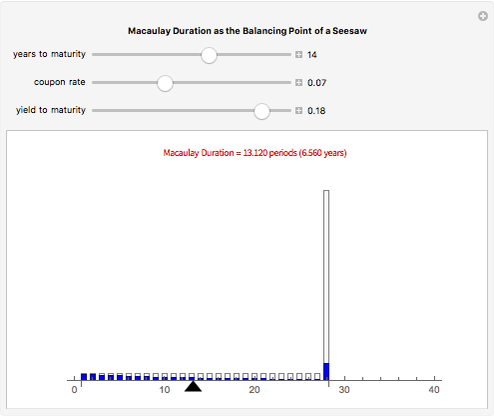
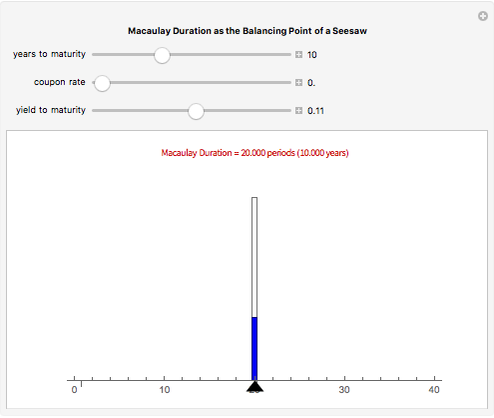
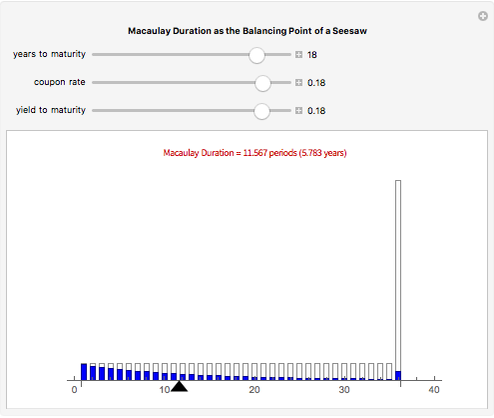
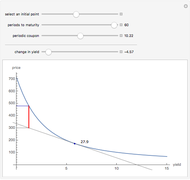
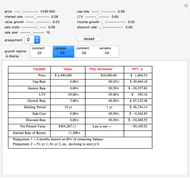
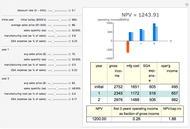
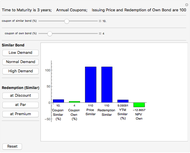
Macaulay's duration is a weighted average of the time until the cash flows are received, where the weights are the present value of the cash flows as a percentage of the security's price. This visualization helps students to understand why increasing the yield and/or coupon rate decreases the duration, while increasing the term to maturity increases the duration (and vice-versa). Imagine a seesaw with several (one for each cash flow) buckets that are the height of the nominal cash flows. The buckets are filled with water to a level that represents the present value of the cash flows. Duration is the location of the fulcrum that results in a balanced seesaw.