Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Maximizing a Bermudan Put with a Single Early-Exercise Temporal Point

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

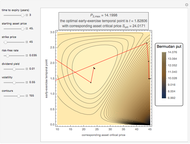
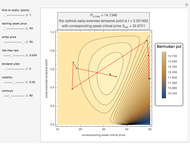
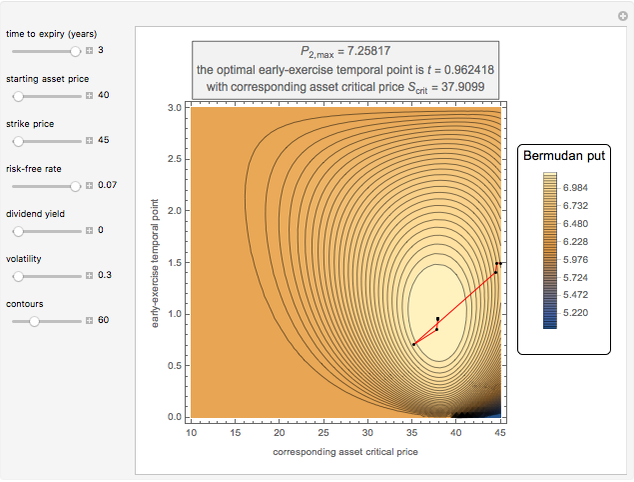
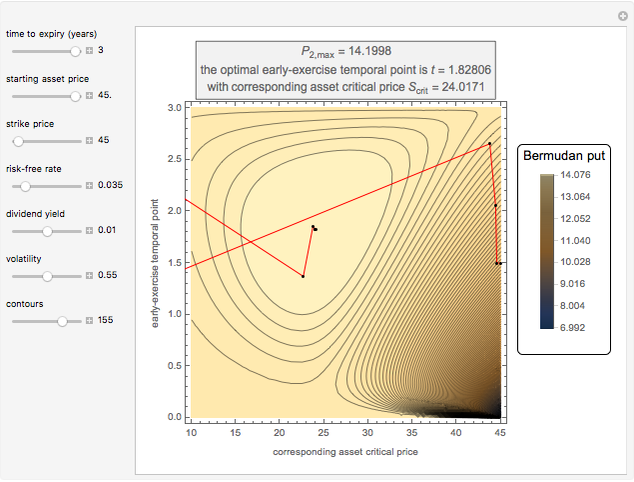
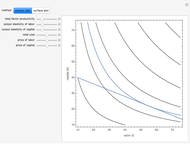
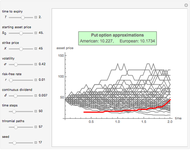
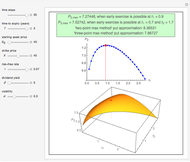
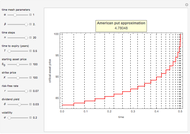
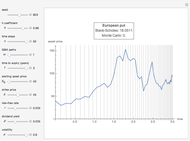
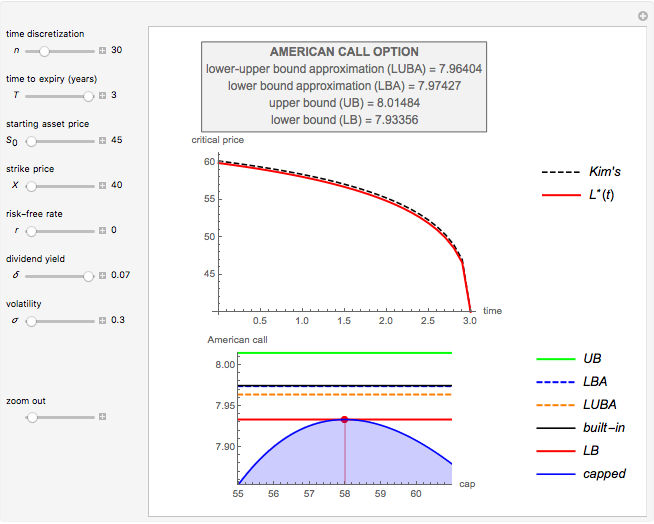
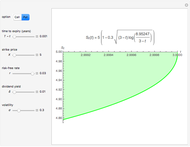
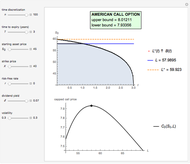
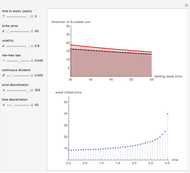
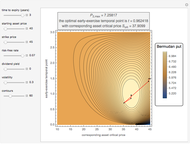
This Demonstration locates the optimal early-exercise temporal point and the corresponding asset critical price that maximize the value of a Bermudan put with a single early-exercise temporal point. Bermudan options can be exercised only on predetermined temporal points and are considered a combination of American and European options. American options are exercisable anytime up to the date of expiration, while European options are exercisable only at the date of expiration. Bermudan options are exercisable at the date of expiration and on certain specified time points that occur between the option purchase date and the date of expiration.

[more]

Use the controls to select the option parameters and contours, and then monitor the steps to optimization; the default coordinates for the starting point are the strike price and the midlife of the option. You can change the default starting point in the code and monitor how optimization is reached.

[less]

Contributed by: Michail Bozoudis (September 2014)
Suggested by: Michail Boutsikas
Open content licensed under CC BY-NC-SA

Snapshots

Details

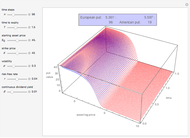
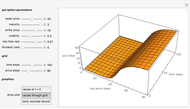
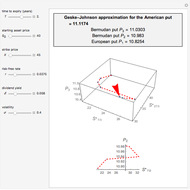
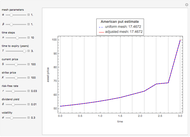
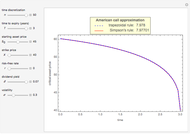
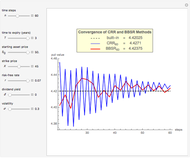
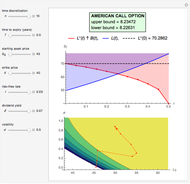
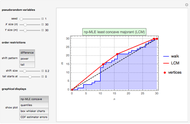
The Geske–Johnson analytical formula [1] is applied to estimate the payoff function of the Bermudan put. The goal of the optimization process is to find the early-exercise time point at which the payoff function of the option is maximized; this time point is related to an asset critical price, as in the case of American options.

Geske and Johnson, in the "G-J" method [1], apply Richardson extrapolation on uniformly time-discretized Bermudan options to approximate the value of an American option. Bunch and Johnson, in the "two-point maximum" and "three-point maximum" approximation methods [2], suggest using optimally time-discretized Bermudan options instead, in order to get a better approximation for the American option.

References

[1] R. Geske and H. Johnson, "The American Put Option Valued Analytically," The Journal of Finance, 39(5), 1984 pp. 1511–1524. doi:10.1111/j.1540-6261.1984.tb04921.x.

[2] D. Bunch and H. Johnson, "A Simple and Numerically Efficient Valuation Method for American Puts Using a Modified Geske–Johnson Approach," The Journal of Finance, 47(2), 1992 pp. 809–816. doi:10.1111/j.1540-6261.1992.tb04412.x.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send