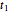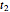Pricing American Options with the Two- and Three-Point Maximum Methods

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
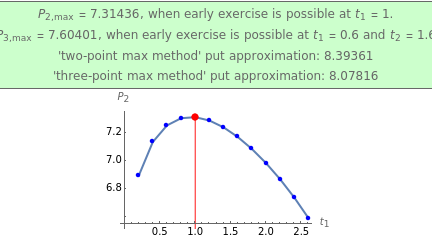
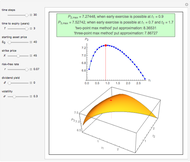
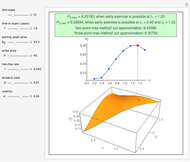
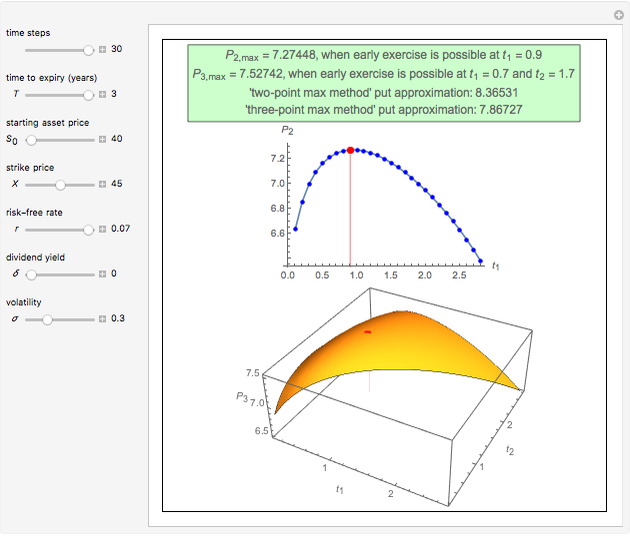
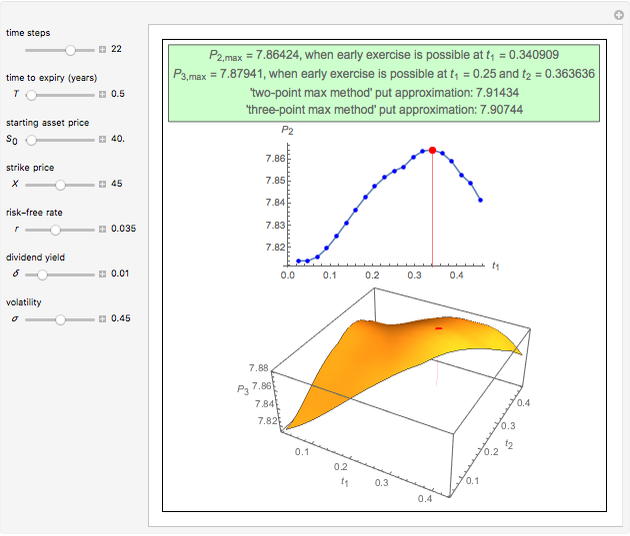
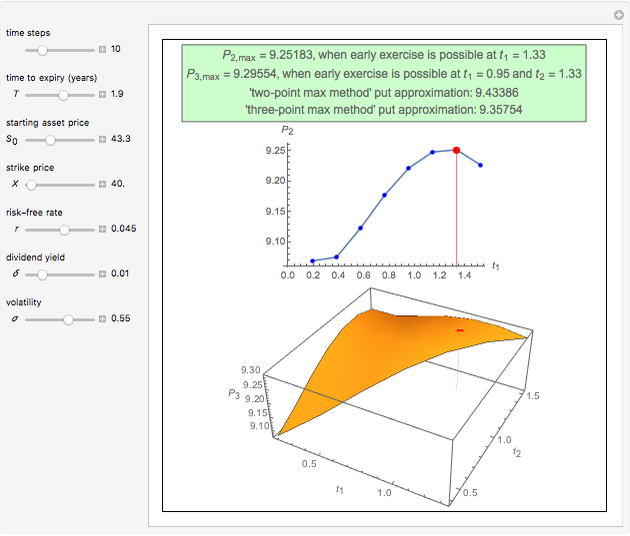
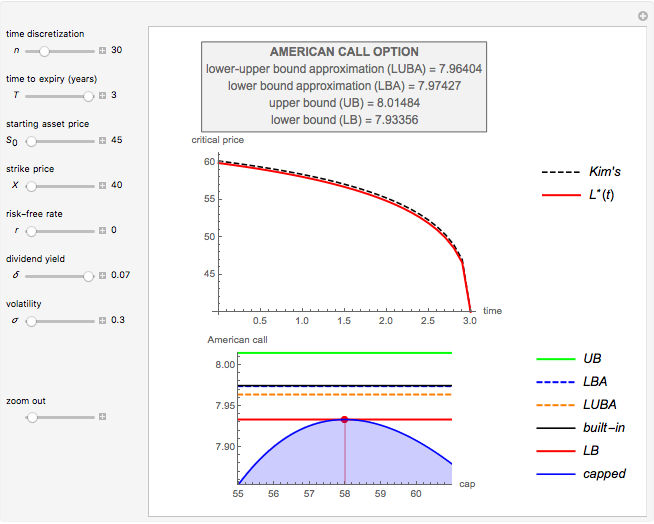
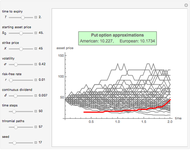
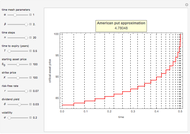
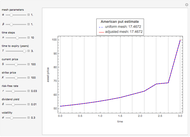
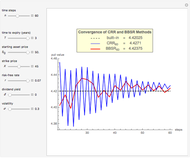
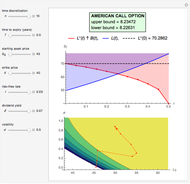
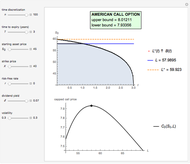
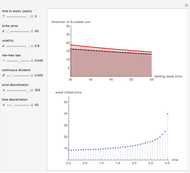
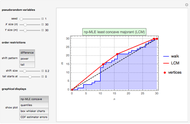
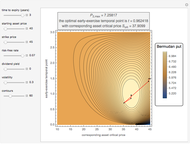
This Demonstration shows the application of the "two-point maximum" and "three-point maximum" methods [2] in order to approximate the value of an American put. The Demonstration uses the trinomial method [3] and the fact that Bermudan options approximate American options to locate the optimal early exercise temporal points and estimate the values 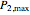 and
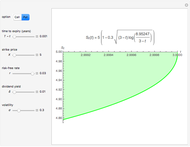
and 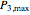 . Use the controllers to set the time discretization for the trinomial tree and the American option parameters.
. Use the controllers to set the time discretization for the trinomial tree and the American option parameters.
Contributed by: Michail Bozoudis (August 2014)
Suggested by: Michail Boutsikas
Open content licensed under CC BY-NC-SA
Snapshots
Details
The "two-point maximum" and "three-point maximum" methods [2] derive from the analytical method [1], which uses the values of
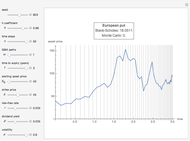
• a European put option 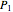 , which can only be exercised at its maturity
, which can only be exercised at its maturity 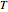 ,
,
• a Bermudan put option 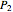 , which can be exercised at
, which can be exercised at 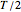 or
or 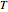 , and
, and
• a Bermudan put option 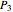 , which can be exercised at
, which can be exercised at 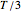 ,
, 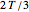 , or
, or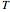 .
.
Then, according to the method [1], Richardson extrapolation is applied twice to approximate the American put value  as
as 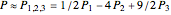 , with an error term of the form:
, with an error term of the form: 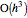 .
.
Instead, the modified "three-point maximum" method [2] uses optimally time-discretized Bermudan options with maximized values 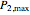 and
and 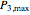 , respectively. When Richardson extrapolation is applied twice, the American put approximation is
, respectively. When Richardson extrapolation is applied twice, the American put approximation is 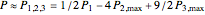 . The error term is again of the form
. The error term is again of the form 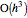 , but in most cases its absolute value is smaller compared to the method [1]. The disadvantage of the modified method [2] compared to the method [1] is that it requires more computational time and effort. The "two-point maximum" method refers to the application of Richardson extrapolation once; the American put approximation is then
, but in most cases its absolute value is smaller compared to the method [1]. The disadvantage of the modified method [2] compared to the method [1] is that it requires more computational time and effort. The "two-point maximum" method refers to the application of Richardson extrapolation once; the American put approximation is then 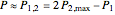 , with an error term of the form
, with an error term of the form 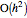 .
.
References
[1] R. Geske and H. Johnson, "The American Put Option Valued Analytically," The Journal of Finance, 39(5), 1984 pp. 1511–1524.
[2] D. Bunch and H. Johnson, "A Simple Numerically Efficient Valuation Method for American Puts Using a Modified Geske–Johnson Approach," The Journal of Finance, 47(2), 1992 pp. 809–816.
[3] P. Boyle, "Option Valuation Using a Three-Jump Process," International Options Journal, 3, 1986 pp. 7–12.
Permanent Citation