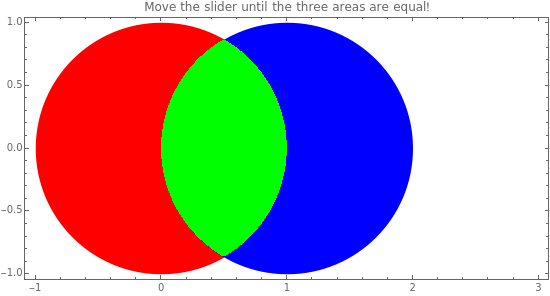
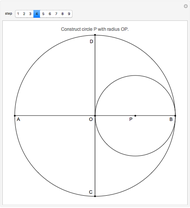
Making the Three Areas Defined by Congruent Overlapping Circles Equal

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
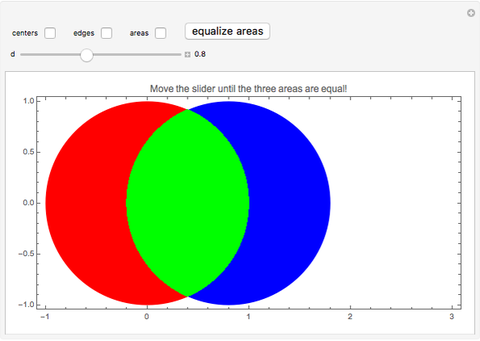
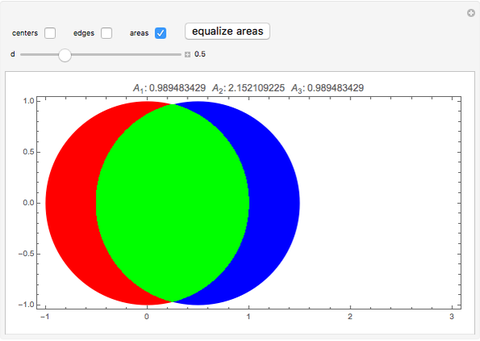
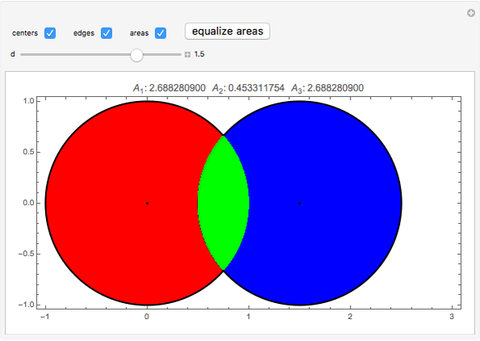
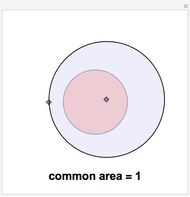
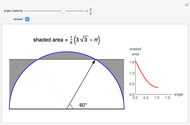
Overlap two congruent circles until the three areas formed are equal. What is the distance between the centers of the two circles, and what is the common area of the three regions? For simplicity, use unit circles (radius 1). The slider moves one of the circles and displays the distance between their centers. The checkboxes allow the display of circle centers, boundaries, and the numerical values of the areas.
Contributed by: Kenneth E. Caviness and Eugene Stewart (September 2014)
Open content licensed under CC BY-NC-SA
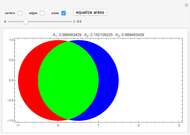
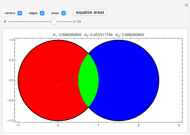
Snapshots
Details
To find the desired overlap area 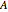 , recall that the area of a circle is
, recall that the area of a circle is 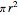 , and then require that
, and then require that 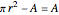 , which can immediately be solved to find that
, which can immediately be solved to find that 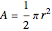 . To find the distance
. To find the distance  , remember that the area of a circular sector of angle
, remember that the area of a circular sector of angle  and radius
and radius  is
is 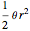 . (This gives the expected area for the whole circle when
. (This gives the expected area for the whole circle when  .) Half of the overlap area can be found by subtracting the area of the isosceles triangle formed by the intersections of the two circles and the center of one of them
.) Half of the overlap area can be found by subtracting the area of the isosceles triangle formed by the intersections of the two circles and the center of one of them 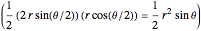 from the sector area, and then doubling gives the area of the lens in terms of
from the sector area, and then doubling gives the area of the lens in terms of  and
and  :
: 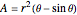 . The distance between the two centers is given by
. The distance between the two centers is given by 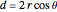 . Setting
. Setting 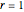 and numerically solving for
and numerically solving for  and
and  gives
gives 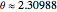 and
and 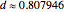 .
.
The overlap area can also be found using integral calculus. For convenience, we again let the radius of the circles be 1. Then the area of each circle is  , and the area of each of the regions must be
, and the area of each of the regions must be 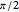 . Let the centers of the two circles be
. Let the centers of the two circles be 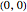 and
and 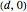 , respectively. The lens is symmetric vertically and horizontally, and one quarter of it is bounded by
, respectively. The lens is symmetric vertically and horizontally, and one quarter of it is bounded by  ,
, 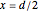 , and the circle
, and the circle 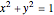 . So
. So 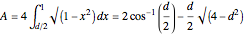 . Setting this equal to
. Setting this equal to 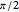 and solving numerically for
and solving numerically for  again gives approximately 0.807946.
again gives approximately 0.807946.
See [1] for a solution arrived at independently.
The alert reader may have recognized the numeric value of the equal areas shown in the display, 1.570796327, as approximately 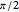 , and we have seen that this is no coincidence. But the numerical value of the distance between circle centers has no immediately obvious significance and cannot even be determined precisely, except as the solution to the transcendental equation above.
, and we have seen that this is no coincidence. But the numerical value of the distance between circle centers has no immediately obvious significance and cannot even be determined precisely, except as the solution to the transcendental equation above.
It is interesting to note that the use of ImplicitRegion and RegionMeasure, new functions introduced in Mathematica 10, immediately gives the formula for the overlap area as a function of separation distance:
Assuming[0
Reference
[1] MathZombie. "How to Create a Two Circle Venn Diagram with 3 Equal Sections?" Mathematics Stack Exchange. (Aug 28, 2014) math.stackexchange.com/questions/769136/how-to-create-a-two-circle-venn-diagram-with-3-equal-sections.
Permanent Citation