Cumulative Area under a Cycloid versus the Area of Its Rolling Circle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
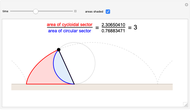
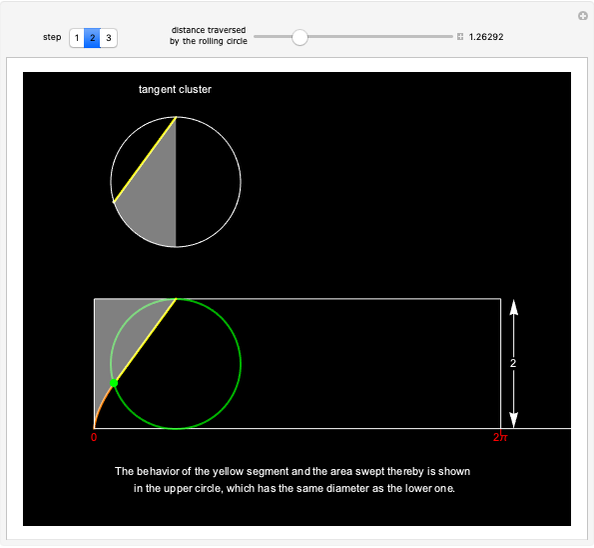
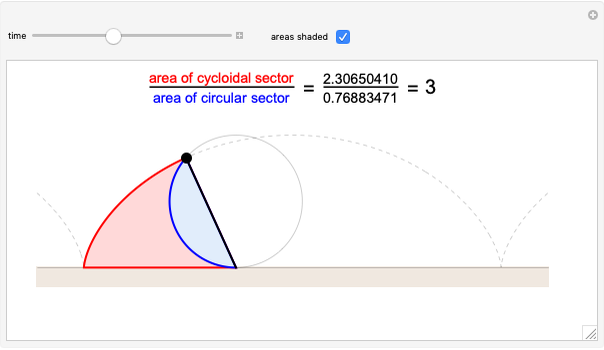
A point on a circle rolling on a straight line without slipping traces out a cycloid. It has long been known that the area under a single arch of the curve is exactly three times the area of the generating circle, but only recently has it been shown that this is a special case of a relationship that holds throughout the cycloid's formation: the ratio of the areas of the cycloidal sector and circular sector remains exactly 3.
Contributed by: Kenneth E. Caviness (June 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The cycloid has been studied by many great mathematicians and scholars, including Galileo Galilei, Pierre de Fermat, René Descartes, Blaise Pascal, Gottfried Wilhelm von Leibniz, and Christopher Wren. If the generating circle has radius  and so area
and so area  , the area under a single hump of the cycloid is
, the area under a single hump of the cycloid is 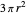 . In this Demonstration, the circle radius is taken to be 1, and thus the area of the circle is
. In this Demonstration, the circle radius is taken to be 1, and thus the area of the circle is 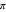 and the area under the cycloid
and the area under the cycloid  .
.
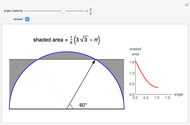
Snapshot 1: the areas of a single hump of a cycloid and of the generating circle, shaded and outlined in red and blue, respectively
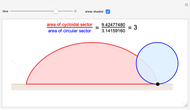
A recent, more general, result relates the areas of the part of the circle that has rolled so far and the cycloidal sector generated up to that point. The controls let you see the areas concerned (or their outlines) at any time during the cycle. Both the cycloidal sector and the portion of the circle bounded by the arc that has been in contact with the floor are bounded on the right by the line segment between the generating point and the circle's point of contact with the floor, and by construction the circular arc has the same length as the horizontal boundary of the cycloidal section, the part of the floor that has been in contact with the circle. It is visually clear that the 3:1 ratio that holds for the complete cycloid hump and whole circle must also hold for the partial areas at the halfway point of construction, but Apostel and Mnatsakanian use geometric considerations in an elegant proof that the result holds in general for all times throughout the cycloid's generation. Thus the classic area theorem becomes a special case of the new theorem.
Standard integration techniques give 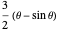 and
and 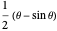 for the cycloidal sector area and the circular sector area, respectively, where
for the cycloidal sector area and the circular sector area, respectively, where  is the angle through which the circle has rotated so far
is the angle through which the circle has rotated so far  .
.
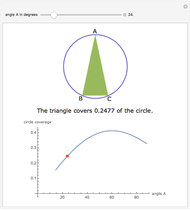
Snapshot 2: the areas of the part of the cycloid generated halfway through the cycle and of the part of the generating circle that has been in contact with the floor
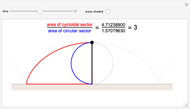
Snapshot 3: the areas of the cycloidal and circular sectors at a time before the halfway mark
Snapshot 4: the areas of the cycloidal and circular sectors at a time after the halfway mark
Reference
[1] T. M. Apostol and M. A. Mnatsakanian, New Horizons in Geometry, Washington, DC: The Mathematical Association of America, 2012.
Permanent Citation