Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Minimum Area between a Semicircle and a Rectangle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

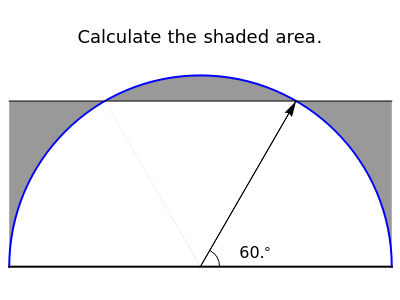
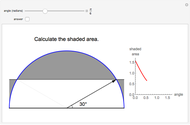
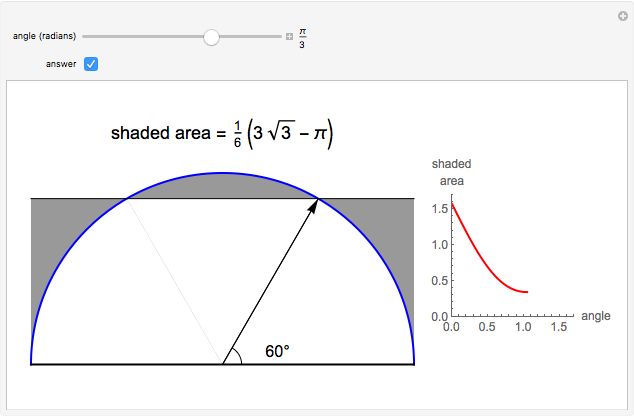
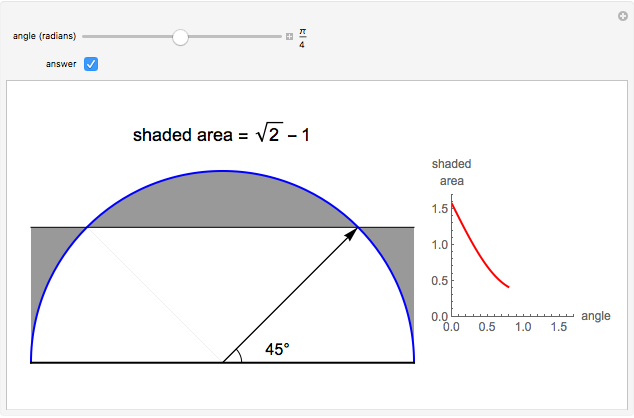
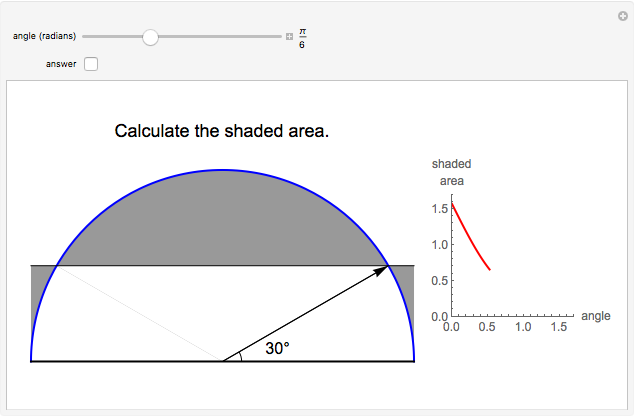
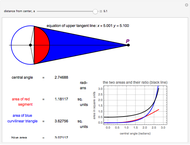
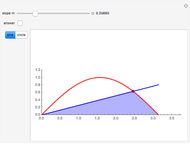
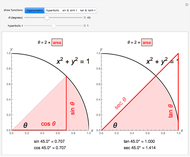
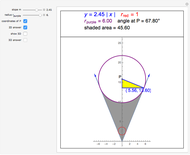
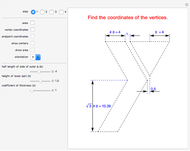
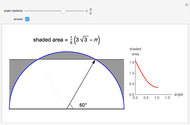
The figure shows a semicircle of radius one and a horizontal line parallel to the diameter. What central angle corresponds to the minimum shaded area? This problem can be solved by either integration or trigonometry. The shaded area is equal to 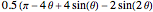, where is the central angle. The minimum shaded area occurs when the central angle is .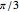

Contributed by: Abraham Gadalla (July 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

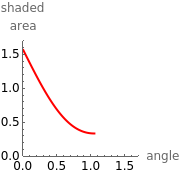
Moving the slider changes the height of the horizontal line and the area of the shaded region. The answer box shows the shaded area at any time. The plot displays the relationship between the shaded area and the central angle.

See [1], Chapter 8, Problem Plus 6.

Reference

[1] J. Stewart, Calculus: Early Transcendentals, 5th ed., Belmont, CA: Brooks/Cole, 2007.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send