Median Split

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
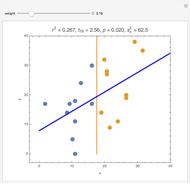
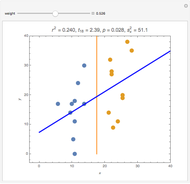
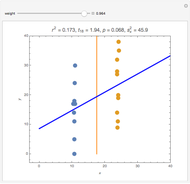
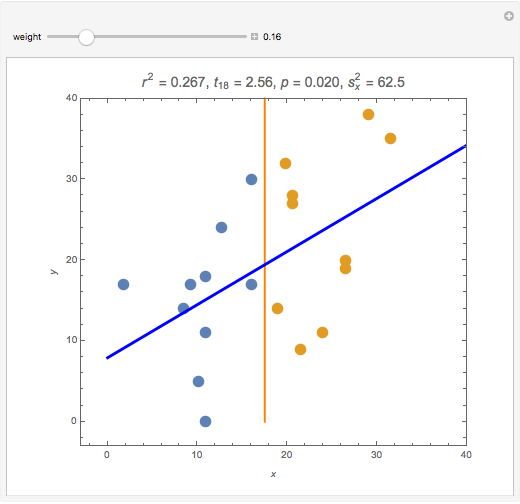
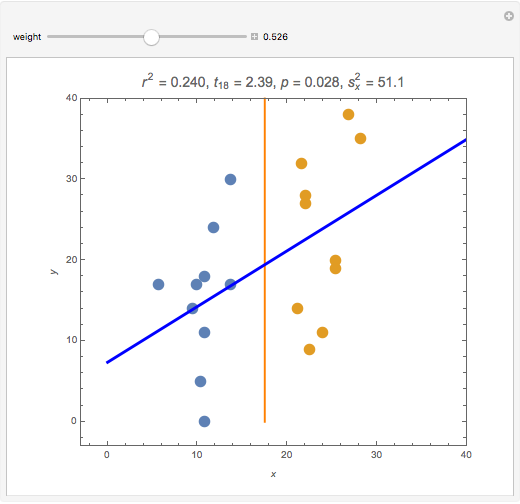
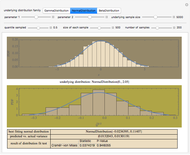
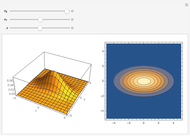
Splitting a continuous variable into two groups at its median is sometimes used in data analysis. On average, splitting a predictor variable  is equivalent in correlation and regression to replacing all the
is equivalent in correlation and regression to replacing all the  values with either the mean
values with either the mean  value for the low group or the high group, as appropriate. Each data value
value for the low group or the high group, as appropriate. Each data value  is replaced by the weighted average
is replaced by the weighted average  , where
, where  is the mean for the group containing
is the mean for the group containing  and
and  is a weight value with
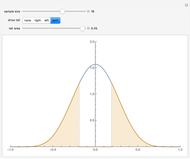
is a weight value with  . Moving the weight slider to the right moves the
. Moving the weight slider to the right moves the  values toward a median split. Observe the decrease in
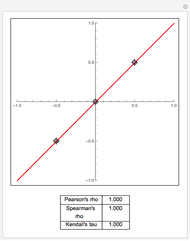
values toward a median split. Observe the decrease in  , the
, the  -statistic, its
-statistic, its  -value, and the predictor's variance as the data is moved towards the equivalent of a median split. Much is lost and nothing gained by a median split.
-value, and the predictor's variance as the data is moved towards the equivalent of a median split. Much is lost and nothing gained by a median split.
Contributed by: Gary McClelland (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
It is interesting to observe the movement of points near each other and near the median. Moving the slider from left to right exaggerates the difference between those observations. At the same time, extreme observations are grouped together with observations near the median as the slider moves from left to right. Exaggerating the difference between observations that were originally close together while at the same time minimizing the differences between observations that were originally very far apart cannot possibly be a useful strategy for data analysis.
For further consideration of this example and other negative consequences of dichotomizing continuous variables, see:
J. R. Irwin and G. H. McClelland, "Negative Consequences of Dichotomizing Continuous Predictor Variables," Journal of Market Research, 40(3), 2003 pp. 366–371.
R. C. MacCallum, S. Zhang, K. J. Preacher and D. D. Rucker, "On the Practice of Dichotomization of Quantitative Variables," Psychological Methods, 7(1), 2002 pp. 19–40.
Permanent Citation
"Median Split"
http://demonstrations.wolfram.com/MedianSplit/
Wolfram Demonstrations Project
Published: March 7 2011