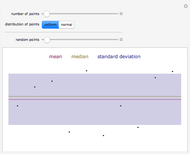
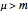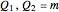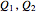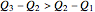Mean, Median, and Quartiles in Skewed Distributions
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
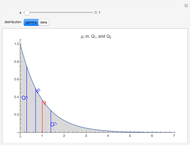
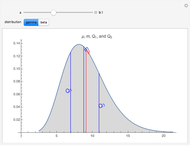
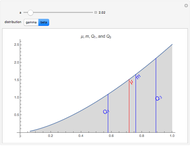
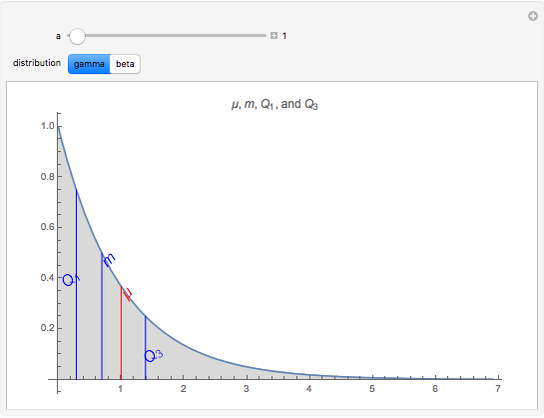
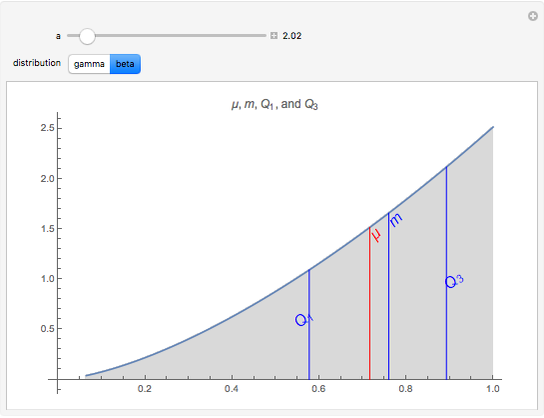
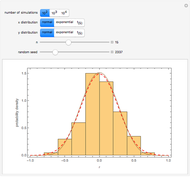
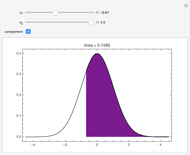
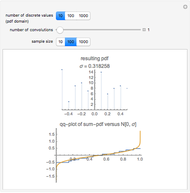
This Demonstration provides a visualization of the relationship between the mean,  , and the median,
, and the median, 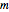 , in positively (right) and negatively (left) skewed distributions, as well as the quartiles
, in positively (right) and negatively (left) skewed distributions, as well as the quartiles 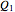 and
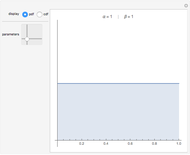
and 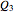 . The positively skewed distributions used are the family of gamma distributions with unit variance and shape parameter
. The positively skewed distributions used are the family of gamma distributions with unit variance and shape parameter  . Beta distributions with parameters
. Beta distributions with parameters  are used for the negatively skewed distributions.
are used for the negatively skewed distributions.
Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation