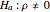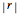Null Distribution of the Correlation Coefficient

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
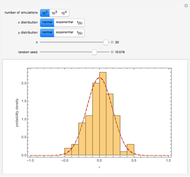
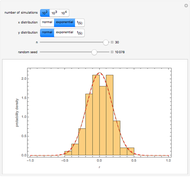
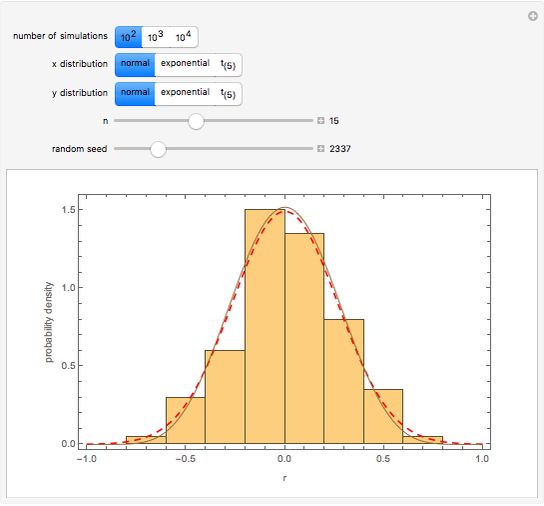
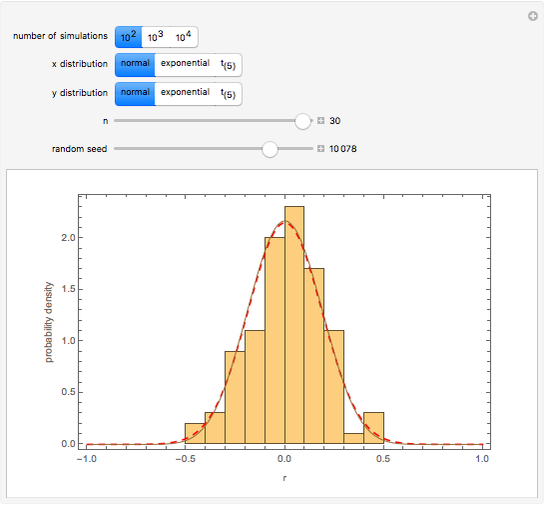
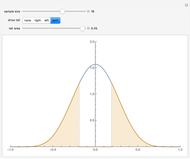
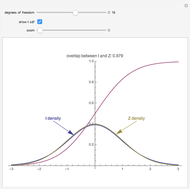
The Pearson correlation coefficient, 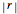 , is considered in most introductory statistics courses. One of the questions students may ask is how large
, is considered in most introductory statistics courses. One of the questions students may ask is how large  needs to be before it is likely to be important. Before presenting a formal significance test, it is helpful to show some simulations.
needs to be before it is likely to be important. Before presenting a formal significance test, it is helpful to show some simulations.
Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation
"Null Distribution of the Correlation Coefficient"
http://demonstrations.wolfram.com/NullDistributionOfTheCorrelationCoefficient/
Wolfram Demonstrations Project
Published: March 7 2011