Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Michaelis-Menten Kinetics in a Chemostat

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

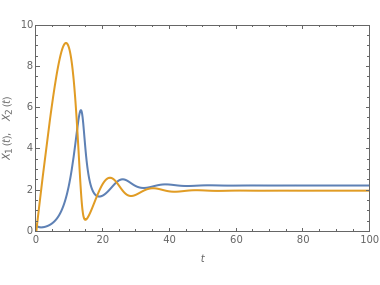
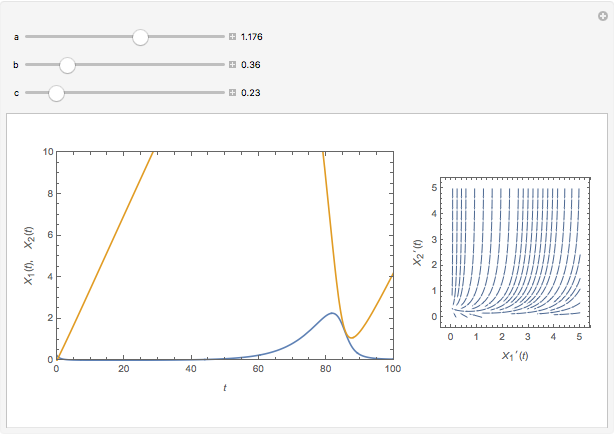
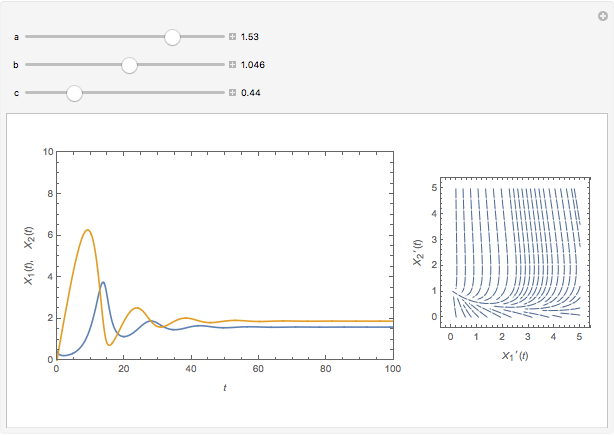
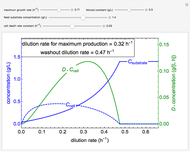
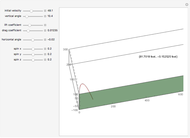
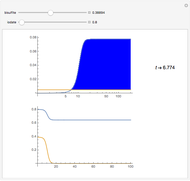
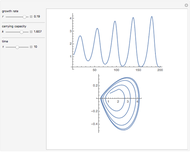
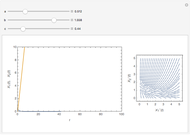
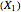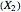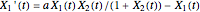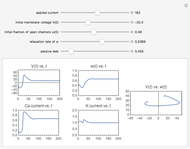
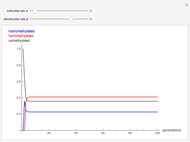
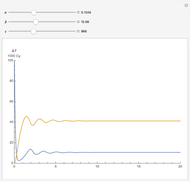
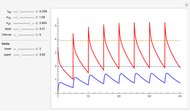
The concentration of an organism culture grows in the presence of nutrient concentration at a rate described by the Michaelis–Menten scheme. In dimensionless form the kinetic equations are: , 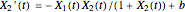. The time evolution of the two concentrations is presented as a function of the growth constant , the nutrient flux, , and the initial concentration, . The phase plane map of these equations is shown simultaneously.

Contributed by: Benson R. Sundheim (August 2011)
Open content licensed under CC BY-NC-SA

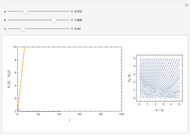
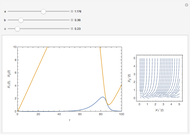
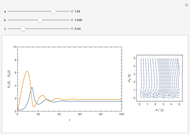
Snapshots

Details

Varying the three parameters permits the study of such features as stable versus unstable equilibrium, steady state, and threshold concentration. Viewing the phase plane map simultaneously permits correlating these with features such as condensation points and nullclines.

References

[1] A. Novick and L. Szilard, "Description of the Chemostat," Science, 112, 1950 pp. 715–716.

[2] L. Michaelis and M. L. Menten, "Die Kinetik der Invertinwirkung," Biochem. Z., 49, 1913 pp. 333–369.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send