Monodromy of z^n + b z + 1 = 0

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
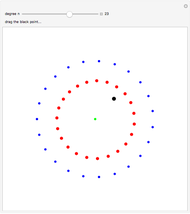
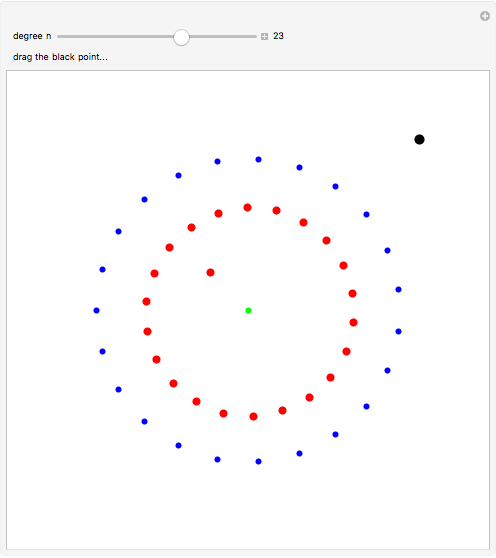
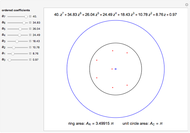
The complex roots of the equation 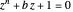 are displayed as red dots. The blue dots correspond to the branching points, that is, to such values of
are displayed as red dots. The blue dots correspond to the branching points, that is, to such values of  that the equation has a double root. The black dot corresponds to
that the equation has a double root. The black dot corresponds to  , which you can drag to see the roots move. In particular, two roots dance around each other and interchange their positions every time
, which you can drag to see the roots move. In particular, two roots dance around each other and interchange their positions every time  moves around a branching point. So, every time
moves around a branching point. So, every time  runs in a loop without hitting any branching points, the roots are permuted. The group generated by such permutations is called the monodromy group of the equation. The parameter
runs in a loop without hitting any branching points, the roots are permuted. The group generated by such permutations is called the monodromy group of the equation. The parameter  and the branching points are displayed at a larger scale to keep them well separated from the roots. The green dot shows
and the branching points are displayed at a larger scale to keep them well separated from the roots. The green dot shows 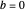 .
.
Contributed by: Michael Livshits (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
While playing with this Demonstration you can see that all the permutations of the roots can be realized by dragging  along judiciously chosen loops. In particular, this means that the monodromy group of the equation
along judiciously chosen loops. In particular, this means that the monodromy group of the equation 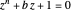 is the group of all the permutations of
is the group of all the permutations of  elements. That implies that when
elements. That implies that when 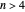 , the equation cannot be solved by an explicit formula that involves radicals and rational expressions, as was proved by Niels Henrik Abel. His proof was topological in nature, and his ideas were further developed by Vladimir Arnold and more recently by his former student Askold Khovanskii, as indicated in his appendix to the book by V. B. Alekseev, Abel's Theorem in Problems and Solutions, Dordrecht, The Nethelands: Kluwer Academic Publishers, 2004, which is a nice exposition based on the lectures given by Vladimir Arnold in the 1963–1964 school year to high school students (Alekseev was one of them) in Moscow. Khovanskii showed that no explicit formula for the solutions of the equation
, the equation cannot be solved by an explicit formula that involves radicals and rational expressions, as was proved by Niels Henrik Abel. His proof was topological in nature, and his ideas were further developed by Vladimir Arnold and more recently by his former student Askold Khovanskii, as indicated in his appendix to the book by V. B. Alekseev, Abel's Theorem in Problems and Solutions, Dordrecht, The Nethelands: Kluwer Academic Publishers, 2004, which is a nice exposition based on the lectures given by Vladimir Arnold in the 1963–1964 school year to high school students (Alekseev was one of them) in Moscow. Khovanskii showed that no explicit formula for the solutions of the equation  exists, even if we allow the following class of functions to enter into our formulas (in addition to radicals): any single-valued functions with no more than a countable number of singularities, their integrals, and compositions of such functions. You also can find a brief treatment in section 19.1 of B. A. Dubrovin, A. T. Fomenko and S. P. Novikov, Modern Geometry—Methods and Applications: Part II. The Geometry and Topology of Manifolds, New York: Springer-Verlag, 1985. (See also Monodromy.)
exists, even if we allow the following class of functions to enter into our formulas (in addition to radicals): any single-valued functions with no more than a countable number of singularities, their integrals, and compositions of such functions. You also can find a brief treatment in section 19.1 of B. A. Dubrovin, A. T. Fomenko and S. P. Novikov, Modern Geometry—Methods and Applications: Part II. The Geometry and Topology of Manifolds, New York: Springer-Verlag, 1985. (See also Monodromy.)
From a numerical perspective, you may notice that when  is small, the roots are located close to the vertices of a regular
is small, the roots are located close to the vertices of a regular 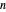 -gon, and when
-gon, and when  is big, there is one small root with the rest located close to the vertices of a regular
is big, there is one small root with the rest located close to the vertices of a regular 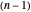 -gon.
-gon.  Why is that? And why is it so difficult to put one root on top of another by dragging
Why is that? And why is it so difficult to put one root on top of another by dragging  ? Try to drag
? Try to drag  in a big circle around all the branch points and notice how the roots move. Can you explain why?
in a big circle around all the branch points and notice how the roots move. Can you explain why?
Permanent Citation