The Action of the Modular Group on the Fundamental Domain

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
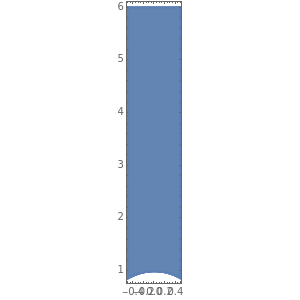
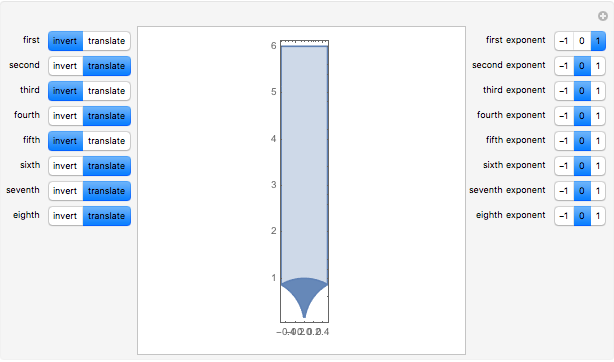
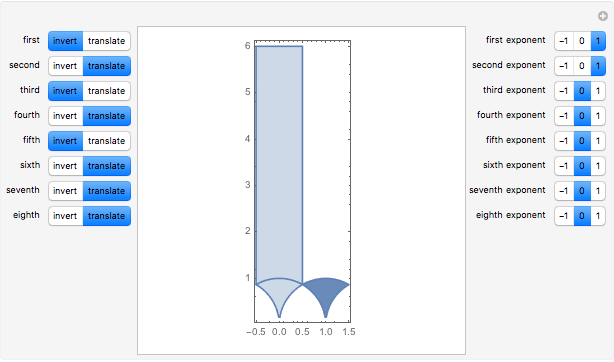
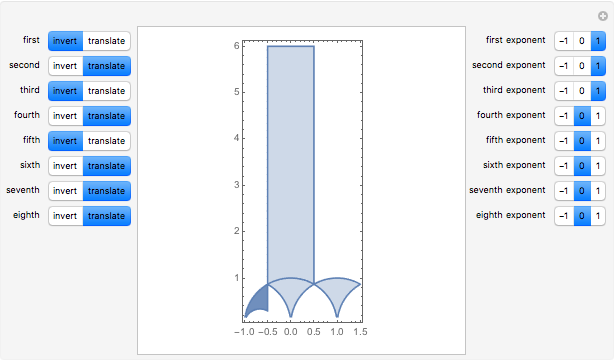
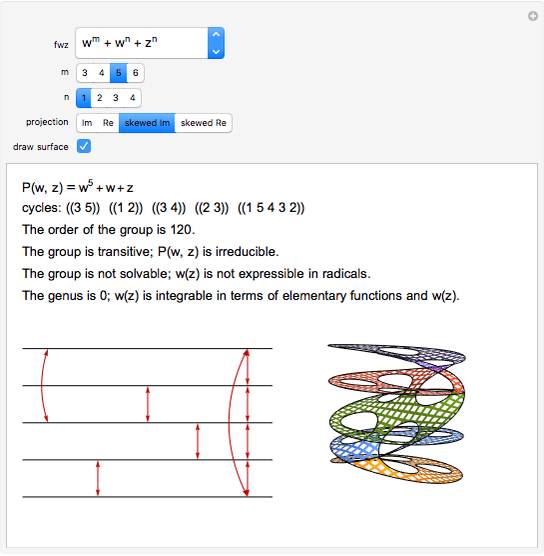
Choose eight transformations from the set of controls on the left. Each transformation can be either an inversion or a translation. Choose the exponent of each of these transformations (-1, 0, or 1) from the set of controls on the right. This Demonstration shows the fundamental domain and its images under the consecutive compositions of the chosen transformations.
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The modular group is the quotient of the group of integer matrices  with
with 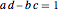 by the subgroup
by the subgroup 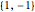 , where
, where 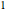 denotes the
denotes the 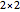 identity matrix. This group acts on the upper half-plane
identity matrix. This group acts on the upper half-plane 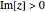 by
by 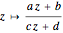 . It turns out that the modular group is generated by just two elements: inversion, given by the matrix
. It turns out that the modular group is generated by just two elements: inversion, given by the matrix 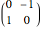 , and translation, given by
, and translation, given by 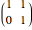 . The fundamental domain is the subset of the upper half-plane
. The fundamental domain is the subset of the upper half-plane 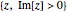 formed by all points
formed by all points  such that
such that 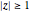 and
and 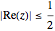 . The action of the modular group tiles the upper half-plane exactly with images of the fundamental domain. This tiling requires the use of the entire infinite fundamental domain, so it cannot be demonstrated by Mathematica. However, this tiling can be approximated by considering the images of a finite part of the fundamental domain under a finite number of compositions
. The action of the modular group tiles the upper half-plane exactly with images of the fundamental domain. This tiling requires the use of the entire infinite fundamental domain, so it cannot be demonstrated by Mathematica. However, this tiling can be approximated by considering the images of a finite part of the fundamental domain under a finite number of compositions 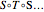 , where each
, where each 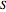 and
and 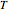 is either a translation by an integer or a reflection.
is either a translation by an integer or a reflection.
Permanent Citation
"The Action of the Modular Group on the Fundamental Domain"
http://demonstrations.wolfram.com/TheActionOfTheModularGroupOnTheFundamentalDomain/
Wolfram Demonstrations Project
Published: March 7 2011