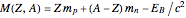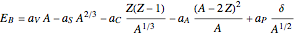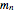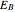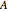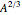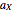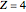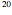Nuclear Liquid-Drop Model Applied to Radioactive Decay Modes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The liquid-drop model in nuclear physics was originally proposed by George Gamow and developed by Hans Bethe and Carl von Weizsäcker in the 1930s. It treats the nucleus as an incompressible fluid of protons and neutrons bound together by the strong nuclear force. It treats the nucleus as an incompressible fluid of protons and neutrons bound together by the strong nuclear force. For a nuclide  containing
containing 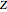 protons and
protons and 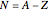 neutronsWeizsäcker's semi-empirical formula for the mass of a nucleus has the form
neutronsWeizsäcker's semi-empirical formula for the mass of a nucleus has the form
Contributed by: S. M. Blinder and B. Ritchie (July 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
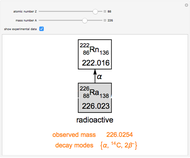
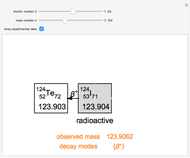
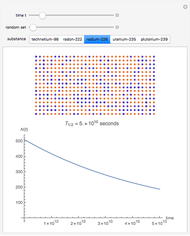
Snapshot 1:  decay of radium to radon; two other decay modes are not predicted by the liquid-drop model
decay of radium to radon; two other decay modes are not predicted by the liquid-drop model
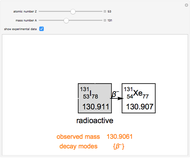
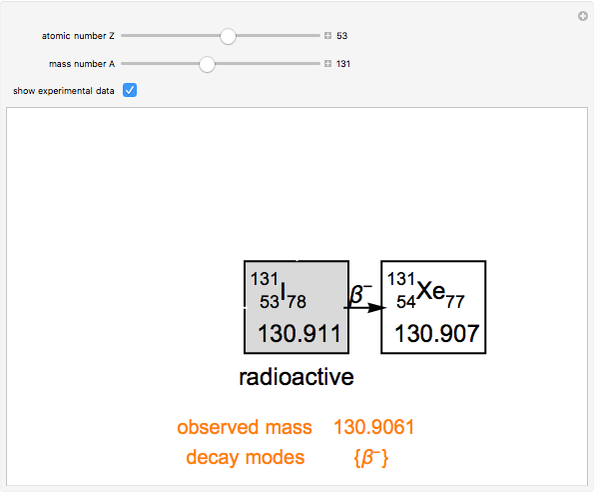
Snapshot 2: nuclei with an excess of neutrons are likely to undergo 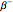 decay
decay
Snapshot 3: whereas those with a neutron deficit will favor 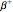 decay
decay
Permanent Citation