Gaussian Laser Modes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
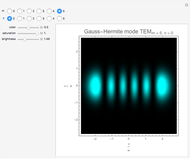
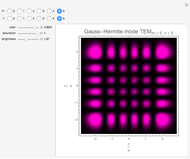
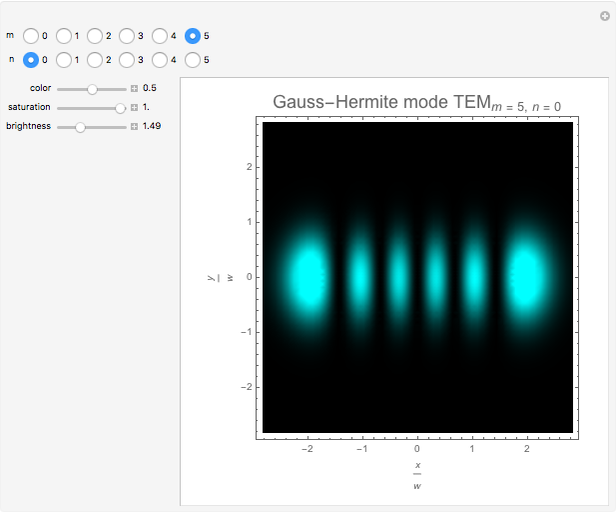
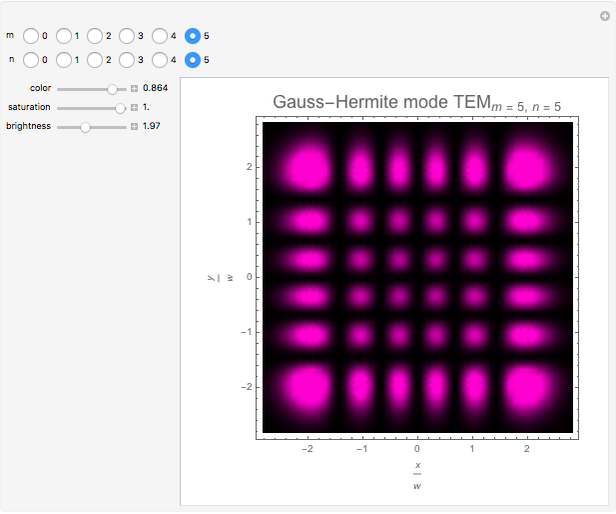
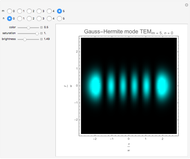
This Demonstration considers the intensity distribution of Hermite-Gaussian transverse
electromagnetic (TEM) modes produced by a laser. These modes are solutions of the paraxial wave equation in Cartesian coordinates. They represent the transverse ( -
-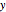 ) intensity distribution of a laser beam propagating in the
) intensity distribution of a laser beam propagating in the  direction.
direction.
Contributed by: Antoine Weis (November 2008)
(Université de Fribourg)
Open content licensed under CC BY-NC-SA
Snapshots
Details
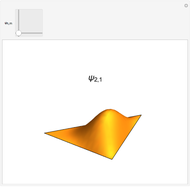
The Hermite-Gaussian modes

are an important family of solutions of the paraxial wave equation

that describes the optical field, that is, the amplitude of the electric field 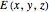 in a laser beam propagating along
in a laser beam propagating along  . The transverse (
. The transverse ( -
-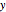 ) intensity distribution of the beam is given by
) intensity distribution of the beam is given by
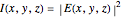 .
.
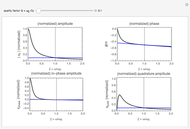
In the above, 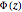 is the phase of the beam, which is irrelevant when discussing the intensity and
is the phase of the beam, which is irrelevant when discussing the intensity and 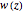 is called the beam radius. As the beam propagates
is called the beam radius. As the beam propagates 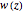 changes in a characteristic manner. However, as seen from the expressions above,
changes in a characteristic manner. However, as seen from the expressions above, 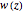 acts as a scaling parameter, so that the transverse beam pattern does not change along the propagation direction; it merely changes its scale, shown in this Demonstration for
acts as a scaling parameter, so that the transverse beam pattern does not change along the propagation direction; it merely changes its scale, shown in this Demonstration for 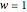 .
.
By setting
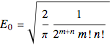 ,
,
the integrated intensity is normalized to yield unit power
 .
.
Permanent Citation