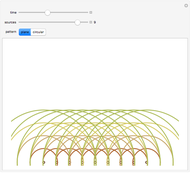
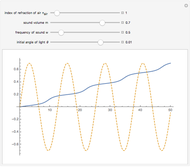
Path of Light through an Acoustic Wave

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
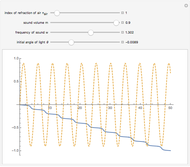
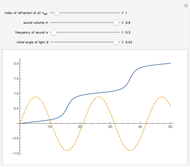
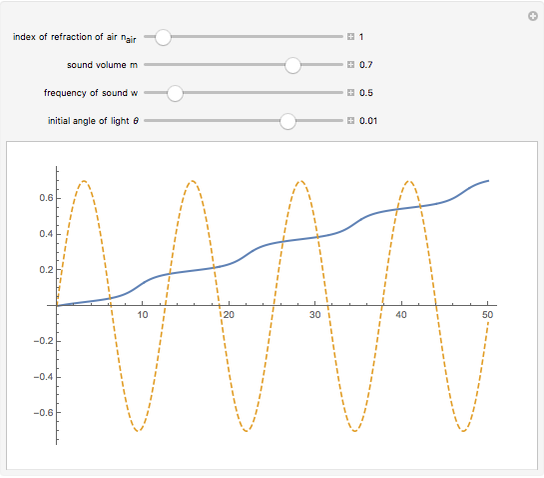
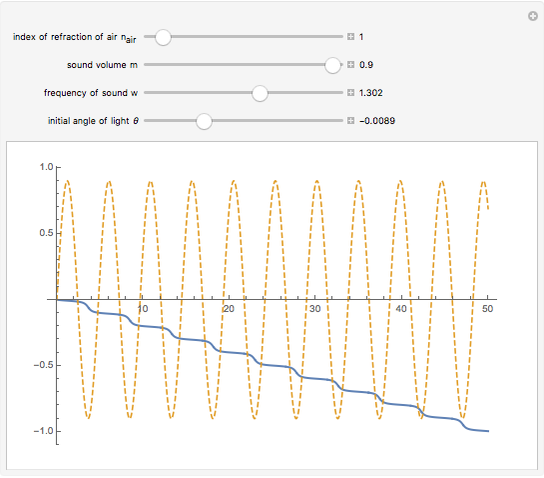
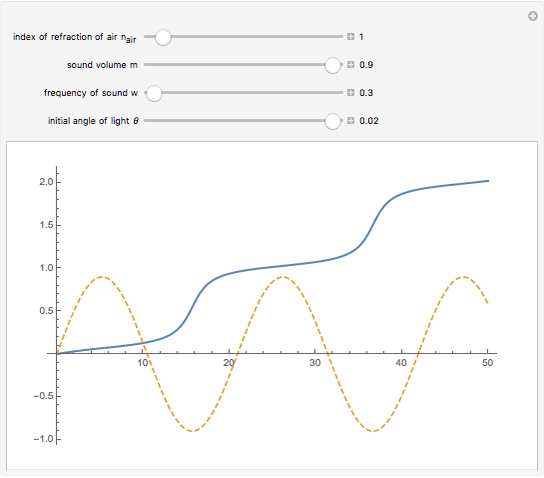
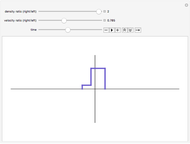
Consider a light wave traveling through a sound wave. Since a sound wave is a fluctuation in air pressure, there is also a fluctuation in the refractive index of the air. This fluctuation in refractive index bends the path of light as it travels through the air.
Contributed by: Brendon O'Leary (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The path of light was calculated by the principle of least time. The time that it takes for light to travel a certain distance can be calculated by the integral
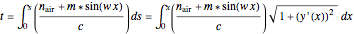 ,
,
such that  is the coordinate along the path of the light.
is the coordinate along the path of the light.
The path 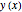 that corresponds to a minimum value of
that corresponds to a minimum value of  was found by solving the Euler–Lagrange equations, which produced this differential equation:
was found by solving the Euler–Lagrange equations, which produced this differential equation:
 .
.
The third-order term was omitted to make the solution to this differential equation more tractable.
This Demonstration shows the path of light (in bold) overlaid with the acoustic wave. The  axis represents distance (in arbitrary units) for the light path and pressure (or index of refraction) of the air, both in arbitrary units. The
axis represents distance (in arbitrary units) for the light path and pressure (or index of refraction) of the air, both in arbitrary units. The  axis is distance for both curves.
axis is distance for both curves.
When the index of refraction of the air increases, the light bends toward the normal of the acoustic wavefront, and when the index of refraction of the air decreases, the light bends away from the normal of the wavefront.
Permanent Citation