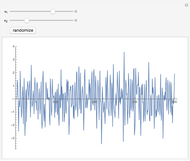
Reverberations in Acoustic Layers

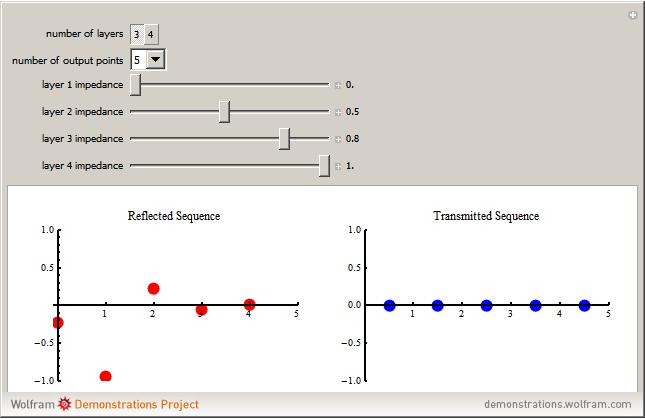
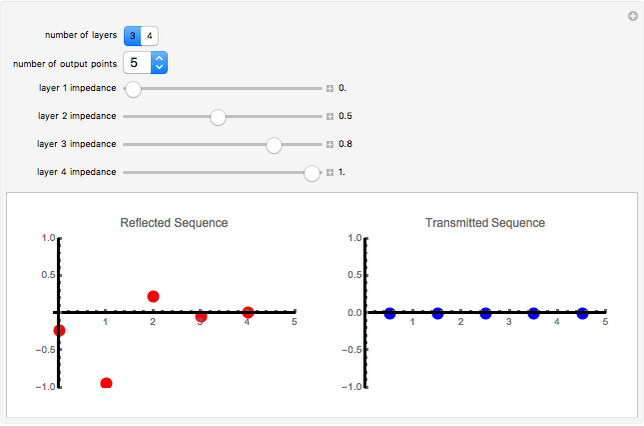
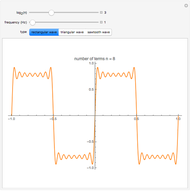
This Demonstration is based on Section 8-3 of Claerbout (1985). (Note an important misprint in eqs. 8-3-8, 9, 10: the should be .)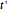

This Demonstration is not intended to handle the trivial case of two half-spaces in contact. A stack of layers is defined such that the bottom and top layers are half-spaces. The travel time across each internal layer is 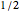unit of time. This is an arbitrary limitation, but it makes the problem tractable. In practice, layers of unequal travel time could be broken into smaller layers wherein the travel times were approximately equal. An acoustic wave with delta pressure amplitude is assumed to impinge on the bottom interface (boundary). The wave reflected into the bottom half-space is given by the 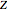-transform (termed in Claerbout). The wave transmitted into the top half-space is given by the 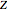-transform (also termed in Clearbout). Inverse transforms of and give the sequences of pulses due to the reverberations in addition to the primary reflected and transmitted pulses. By their nature, each of the inverse transforms is an infinite series; however, the amplitudes of the resulting pulses decay rapidly with time, and only a few generally need to be plotted.

We number the 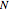layers from the top down. Then the impedances of the layers are used to get the reflection and transmission factors at each interface of a downgoing wave with

,

,

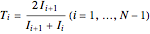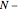where is the impedance and 1 is the number of interfaces. Corresponding factors for an upgoing wave are

,

.

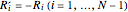Details of forming the general reverberation sequences from these factors are given in Claerbout. From this formulation, one can see that the impedances only need to be given relatively; thus, slider bar scales from 0 (vacuum) to 1 (rigid) are used for all the impedances. In this Demonstration, only three-layer and four-layer models are allowed. Little or no insight is gained into reverberations by including larger numbers of layers, and the computation time will greatly increase with larger numbers.

J. F. Claerbout, Fundamentals of Geophysical Data Processing: With Applications to Petroleum Prospecting, Palo Alto, CA: Blackwell, 1985.