Platonic Solids

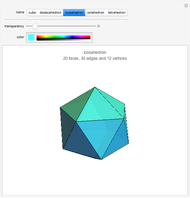
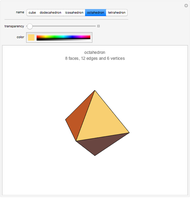
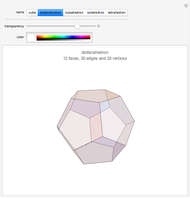
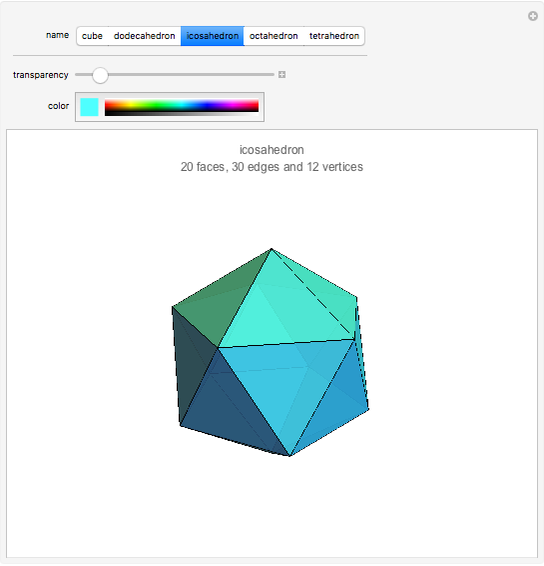
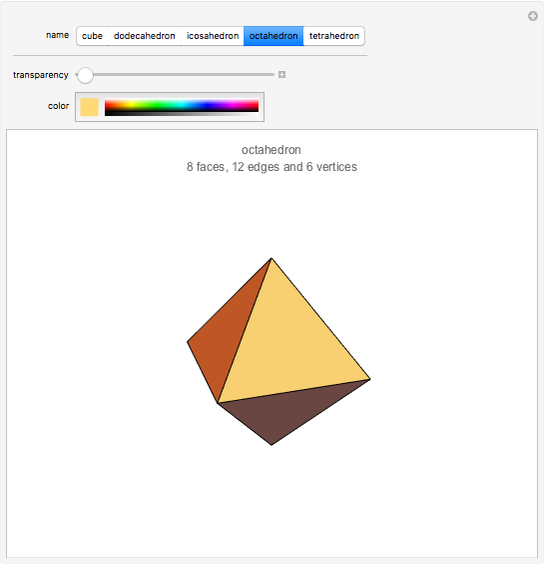
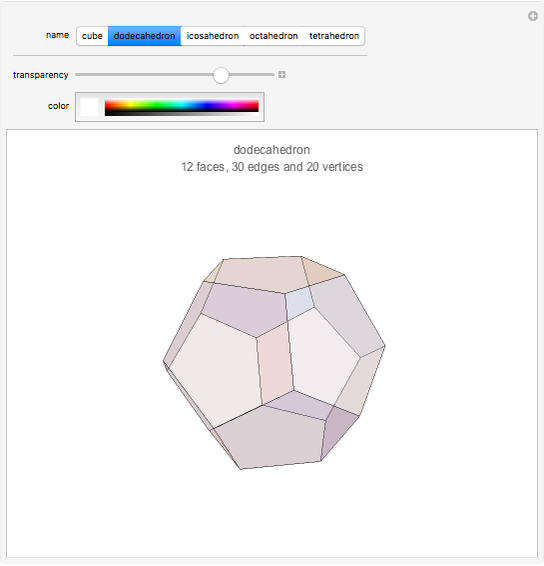
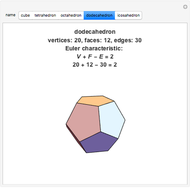
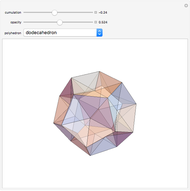
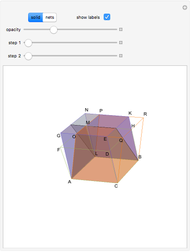
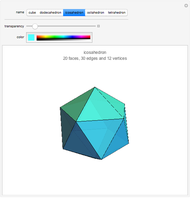
There are only five convex polyhedra with identical regular convex faces, as proved in Euclid's Elements. All their vertices lie on a sphere, all their faces are tangent to another sphere, all their edges are tangent to a third sphere, all their dihedral and solid angles are equal, and all their vertices are surrounded by the same number of faces.