Mathematica MathWorld Wolfram Science More »

HOME

TOPICS

LATEST

Square Matrix Permutations


	Repeated application of a particular permutation of the elements of an matrix based on traversing diagonals results in the original matrix. The number of iterations for to complete the cycle is the same as the length of the period of the periodic sequence that results from the Fibonacci sequence modulus known as the Pisano period.


	Contributed by: Noel Patson Based on work by: Eric W. Weisstein
	Show Initialization Code

For a 3×3 matrix the permutation takes

into

, for example.

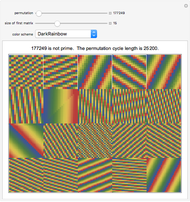
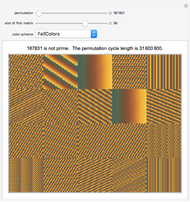
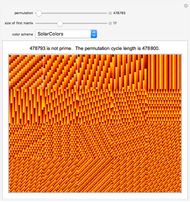
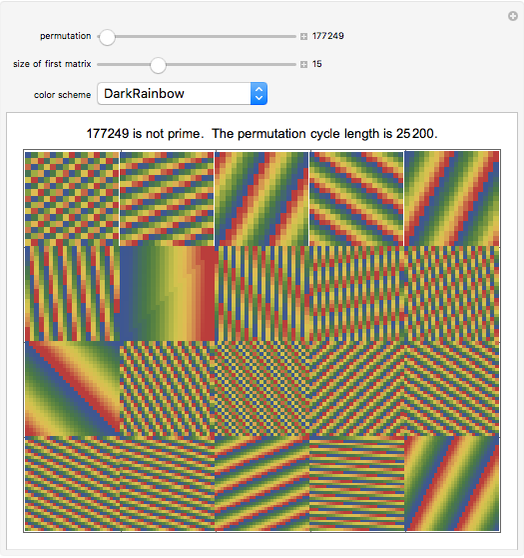
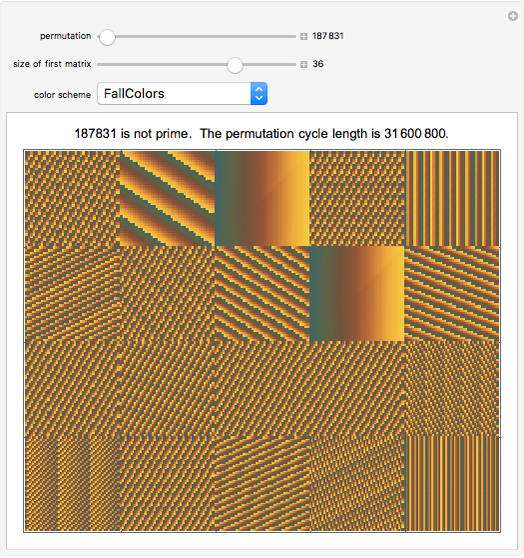
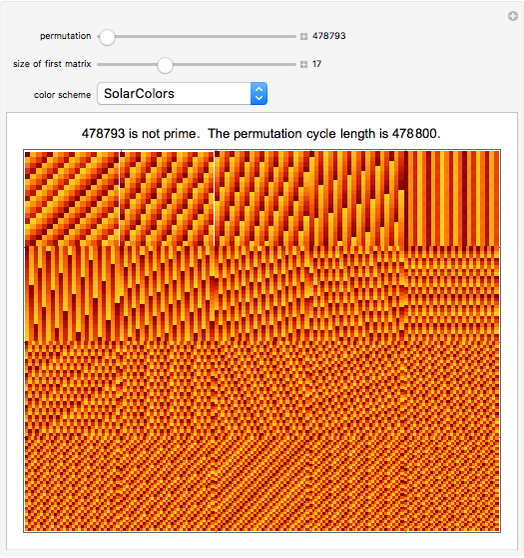
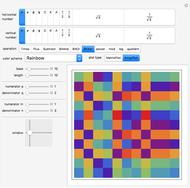
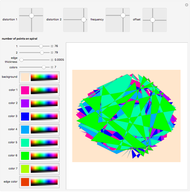
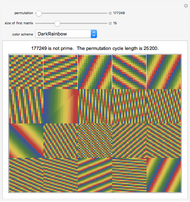
The size of the matrix at the top left is given by the "size of first matrix" slider. This matrix and the next 19 matrices are represented at the same time. Holding the mouse over any matrix reveals its size and the corresponding Pisano period.

Use the "permutation" slider to rearrange the elements of each matrix and watch the matrices synchronize and desynchronize with each other. Choose a different "color scheme" to enhance viewing the weaving patterns.

The "cycle length" is the least common multiple of the 20 Pisano periods corresponding to the 20 displayed matrices.

Reference: Pisano Period and Permutations of n×n Matrices

Pisano Period (Wolfram MathWorld)

"Square Matrix Permutations " from The Wolfram Demonstrations Project
http://demonstrations.wolfram.com/SquareMatrixPermutations/

Contributed by: Noel Patson

Based on work by: Eric W. Weisstein

Report an issue »

Interact with Demonstrations using the latest version of the free Mathematica Player—Download Now

Browse all topics

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

Wolfram Research

Site Index

RSS

Atom