Points and Lines on Folded Paper

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
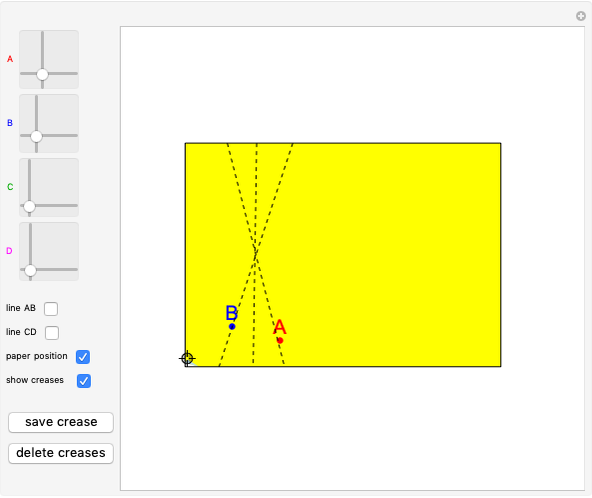
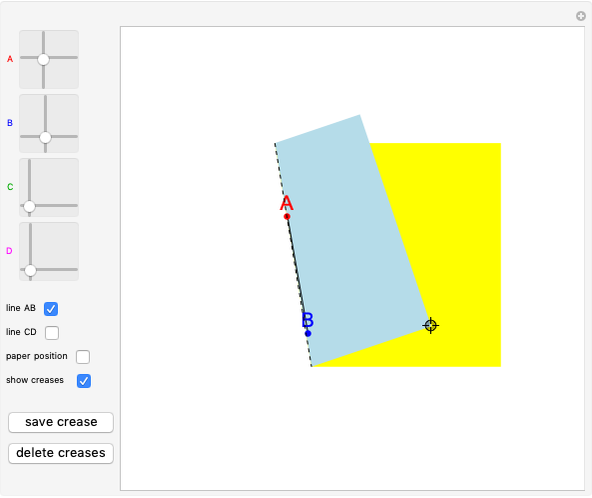
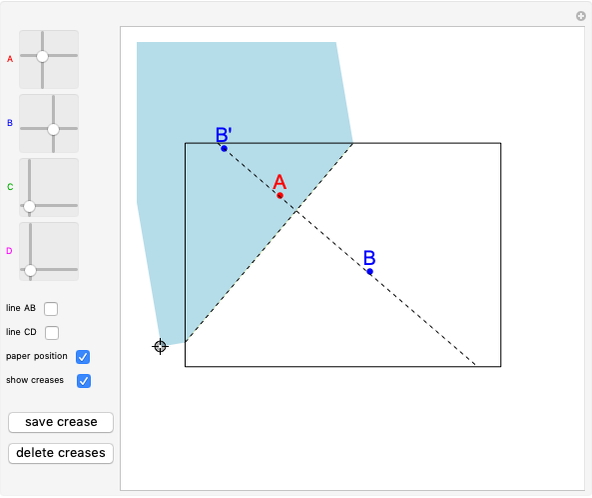
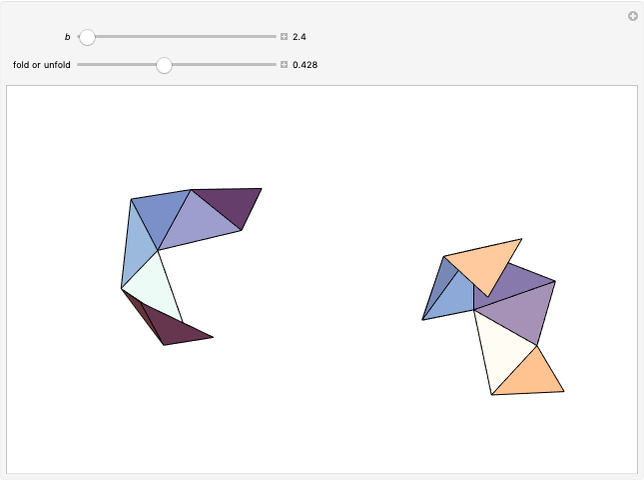
Drag the locator to fold the piece of piece of A4 paper, which is yellow on one side and light blue on the other. You can add points 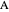 ,
, 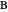 ,
, 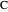 or
or 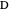 using the 2D sliders on the left. Vary these controls to verify Huzita's axioms.
using the 2D sliders on the left. Vary these controls to verify Huzita's axioms.
Contributed by: Izidor Hafner (March 2019)
Using code by: Borut Levart
Open content licensed under CC BY-NC-SA
Snapshots
Details
Huzita's axioms [1, pp. 285–286]:
A1. Given two points, one can fold a crease line through them.
A2. Given two points, one can fold a crease along their perpendicular bisector, folding one point on top of the other.
A3. Given two lines, one can fold their bisector crease, folding one line on top of the other.
A4. Given a point and a line, one can fold a crease through one point perpendicular to the line, folding the line onto itself.
A5. Given two points and a line, one can fold a crease through one point that maps the other point onto the line.
A6. Given two points and two lines, one can fold a crease that simultaneously maps one point to one line and the other point to the other line.
Reference
[1] E. D. Demaine and J. O'Rourke, Geometric Folding Algorithms: Linkages, Origami, Polyhedra, New York: Cambridge University Press, 2007.
Permanent Citation