No-Three-in-Line Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
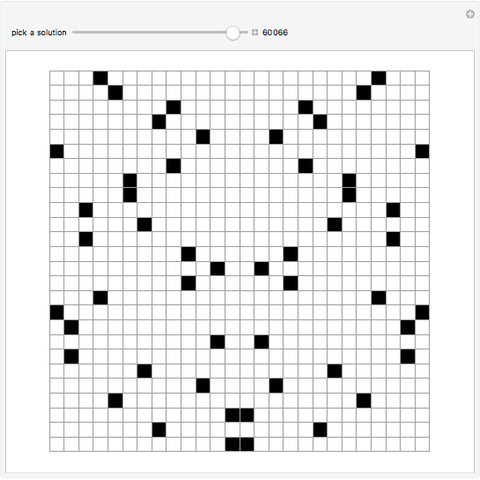
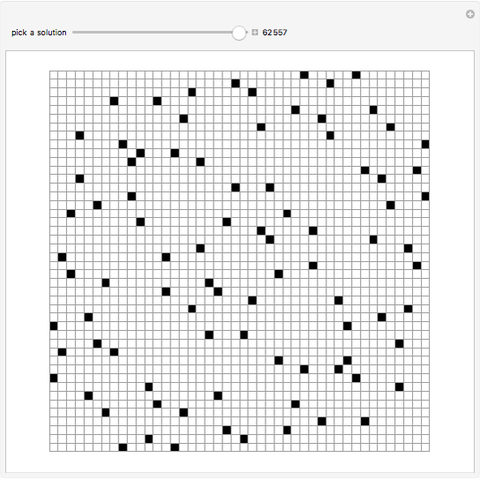
In 1917, Henry Dudeney asked for the maximum number of points selectable from an  ×
× grid so that no three points are collinear. Obviously, no more than two points can be selected from any row or column, so the maximal amount of points is
grid so that no three points are collinear. Obviously, no more than two points can be selected from any row or column, so the maximal amount of points is  . Calling a solution an
. Calling a solution an  ×
× grid with a maximal selection of
grid with a maximal selection of  points with no three points collinear, a 52×52 grid with 104 selected points is the largest known solution. This Demonstration gives all solutions up to order 18×18, and some of the known solutions for larger-sized grids.
points with no three points collinear, a 52×52 grid with 104 selected points is the largest known solution. This Demonstration gives all solutions up to order 18×18, and some of the known solutions for larger-sized grids.
Contributed by: Ed Pegg Jr (November 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Solution data for orders 17 and 18 are from [2]. All other solution data is from [1].
References
[1] A. Flammenkamp. "The No-Three-in-Line Problem." (Mar 3, 1998) wwwhomes.uni-bielefeld.de/achim/cgi/no3in/readme.html.
[2] B. Chaffin. "No Three In Line Problem." (Apr 4, 2006) wso.williams.edu/~bchaffin/no_three_in _line/index.htm.
[3] Wikipedia. "No-Three-in-Line Problem." (Nov 5, 2013) en.wikipedia.org/wiki/No-three-in-line_problem.
Permanent Citation
"No-Three-in-Line Problem"
http://demonstrations.wolfram.com/NoThreeInLineProblem/
Wolfram Demonstrations Project
Published: November 8 2013