The Eneström-Kakeya Bounds for Roots of a Polynomial with Positive Coefficients

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
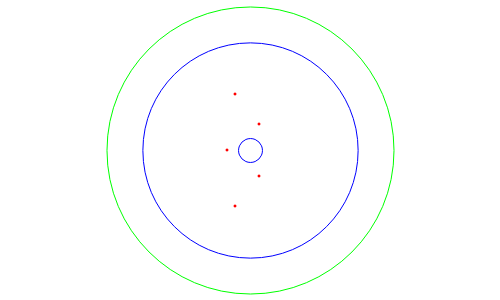
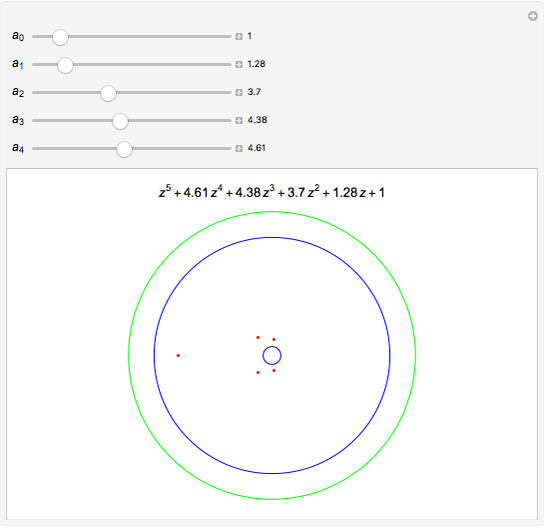
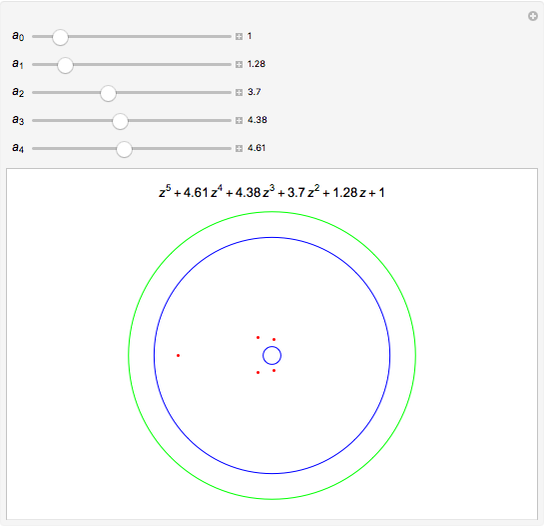
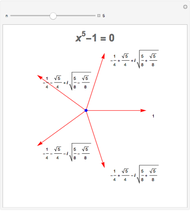
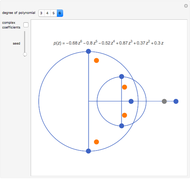
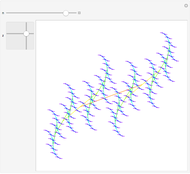
This Demonstration shows some bounds on the roots of a polynomial with positive coefficients of the form 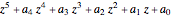 . The green circle (centered at the origin) has radius
. The green circle (centered at the origin) has radius 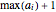 . All roots (represented by the red points) always lie within this circle. This is a bound obtained by applying Rouché's theorem in complex analysis. The two blue circles (centered at the origin) represent the bounds given by the Eneström–Kakeya theorem. The roots always lie between these two circles. By varying the coefficients, we see that for certain polynomials the Eneström–Kakeya bounds are much tighter than the one given by Rouché's theorem, but for other polynomials it can be the other way around.
. All roots (represented by the red points) always lie within this circle. This is a bound obtained by applying Rouché's theorem in complex analysis. The two blue circles (centered at the origin) represent the bounds given by the Eneström–Kakeya theorem. The roots always lie between these two circles. By varying the coefficients, we see that for certain polynomials the Eneström–Kakeya bounds are much tighter than the one given by Rouché's theorem, but for other polynomials it can be the other way around.
Contributed by: Andrzej Kozlowski (November 2011)
Open content licensed under CC BY-NC-SA
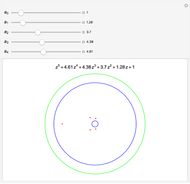
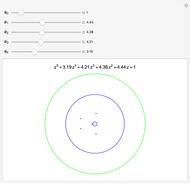
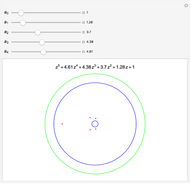
Snapshots
Details
The well-known proof of the fundamental theorem of algebra by means of Rouché's theorem from complex analysis can be extended to give an upper bound on the moduli of the roots. Namely, one can prove that for any polynomial  , exactly
, exactly  roots (counted with multiplicities) are located inside the disk
roots (counted with multiplicities) are located inside the disk  . For polynomials with real positive coefficients, the Eneström–Kakeya theorem states that the moduli of the roots lie between
. For polynomials with real positive coefficients, the Eneström–Kakeya theorem states that the moduli of the roots lie between 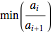 and
and 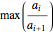 . Both of these results are illustrated in the Demonstration.
. Both of these results are illustrated in the Demonstration.
V. V. Prasolov, Polynomials, Moscow: Moscow Center for Continuous Mathematical Education, 2001 (in Russian).
Permanent Citation