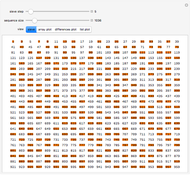
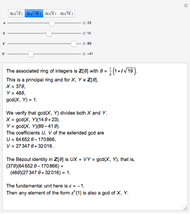
Positive Frobenius Numbers of Three Arguments

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
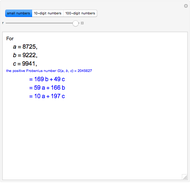
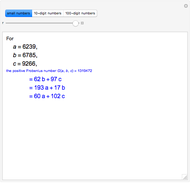
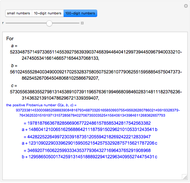
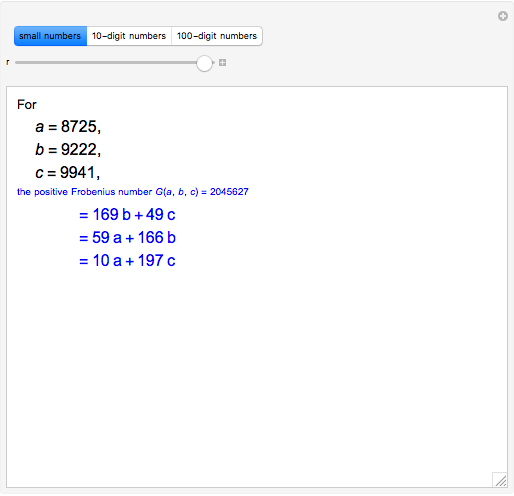
Let  ,
,  ,
,  be three positive integers with
be three positive integers with 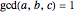 . It is well-known that all sufficiently large integers are representable as positive linear combinations of
. It is well-known that all sufficiently large integers are representable as positive linear combinations of  ,
,  ,
,  . Consider
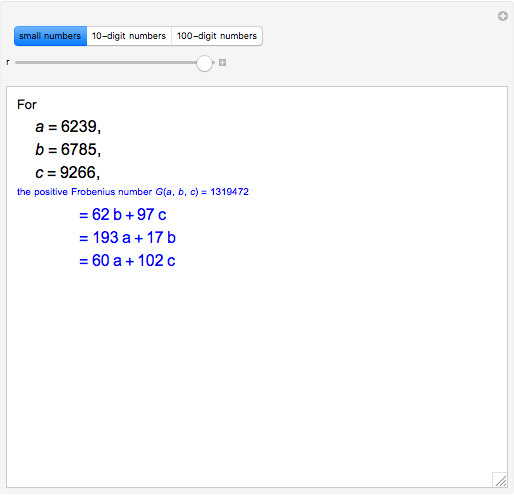
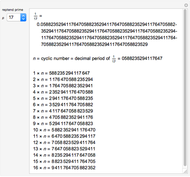
. Consider 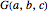 , the positive Frobenius number of
, the positive Frobenius number of  ,
,  ,
,  , defined to be the largest integer not representable as a positive linear combination of
, defined to be the largest integer not representable as a positive linear combination of  ,
,  ,
,  . Then
. Then 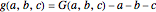 is the usual Frobenius number, that is, the largest integer not representable as a non-negative linear combination
is the usual Frobenius number, that is, the largest integer not representable as a non-negative linear combination  ,
,  ,
,  . (
. (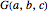 differs from the positive Frobenius number
differs from the positive Frobenius number 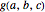 in that multipliers for linear combinations of larger integers are allowed to be zero.) The function
in that multipliers for linear combinations of larger integers are allowed to be zero.) The function 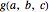 corresponds to the Mathematica built-in function FrobeniusNumber[a,b,c].
corresponds to the Mathematica built-in function FrobeniusNumber[a,b,c].
Contributed by: Abdelwaheb Miled (March 2011)
Open content licensed under CC BY-NC-SA
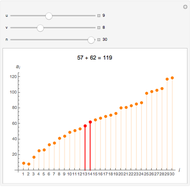
Snapshots
Details
S. M. Johnson, "A Linear Diophantine Problem," Canadian Journal of Mathematics, 12, 1960 pp. 390–398.
A. Miled, "On a Problem of Frobenius in Three Numbers," arXiv.org, 2009.
Permanent Citation