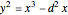Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Congruent Numbers

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

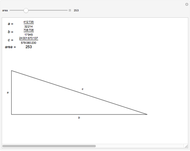
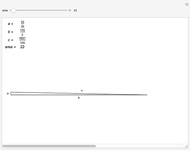
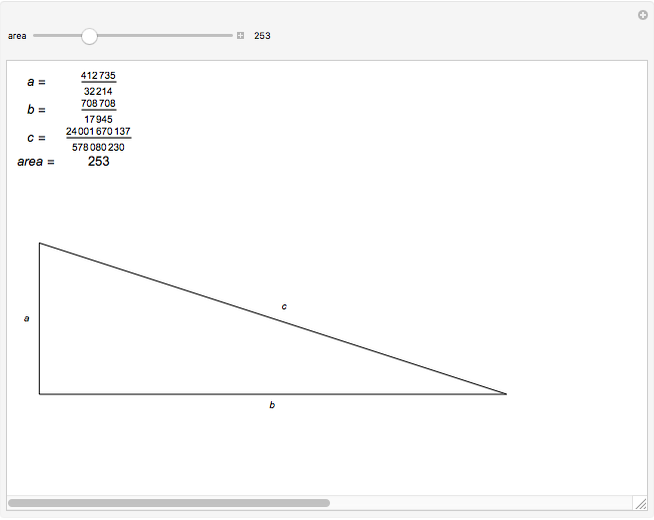
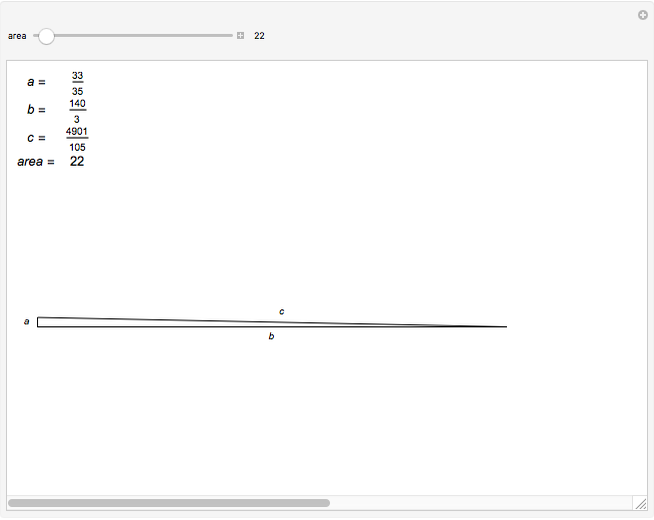
A positive integer is called congruent if it is the area of a right triangle whose side lengths are rational numbers.

[more]

For example, the right triangle with legs 20/7 and 357/5 has area 102, and the hypotenuse 2501/35 is rational, so 102 is a congruent number. This Demonstration shows representative triangles for all known congruent numbers under 1000. Finding a triangle for area is equivalent to solving the elliptic curve . Completely solving this problem is similar to solving the Birch and Swinnerton-Dyer conjecture, which is an unsolved problem with a million-dollar prize.

[less]

Contributed by: Ed Pegg Jr (November 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Data for these triangles is from [1].

References

[1] M. Fiorentini. "Numeri Congruenti Minori di 1000." bitman.name/math/table/29.

[2] Wikipedia. "Congruent Number." (Mar 14, 2013) en.wikipedia.org/wiki/Congruent_number.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send