Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

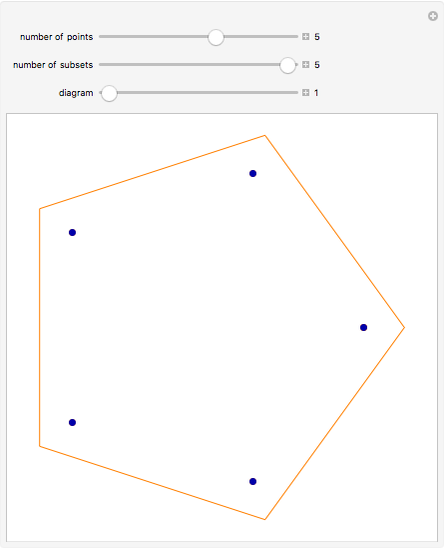
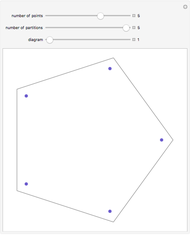
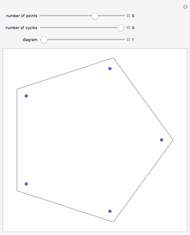
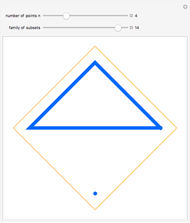
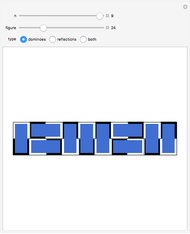
Lah Numbers

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

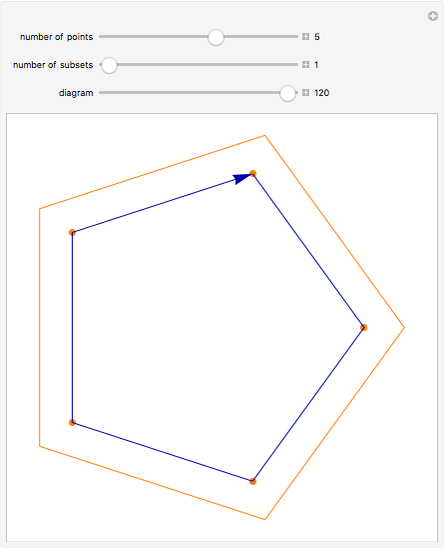
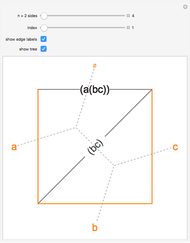
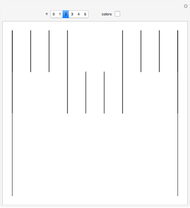
The Lah numbers 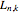count the number of ways to partition a list of elements into disjoint, nonempty subsets, where the order of elements in a subset is significant. This is in contrast to the Stirling numbers of the second kind, which count such partitions where the order of elements in a subset does not matter, and Stirling numbers of the first kind, which consider the cycles of a permutation. This Demonstration illustrates the different partitions that Lah numbers count.

Contributed by: Robert Dickau (February 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

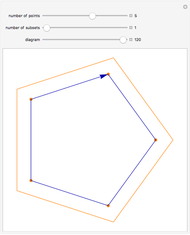
Snapshot 1: 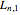counts the number of ways to partition elements into only one list. Because the order of elements in the list is significant, and there are 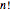ways to order elements, .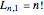

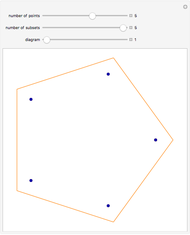
Snapshot 2: Similarly, 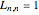because there is only one way to partition elements into nonempty subsets (the order of the subsets themselves does not matter).

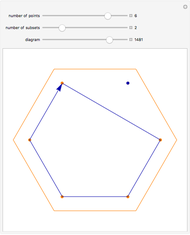
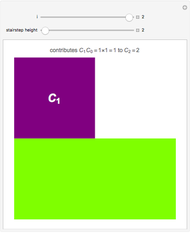
Snapshot 3: The Lah numbers can be computed recursively; by comparing Snapshot 1 and Snapshot 3, it is apparent that and 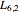are related.

Reference

[1] J. Riordan, Introduction to Combinatorial Analysis, New York: John Wiley, 1958 pp. 43–44.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send