Probability Logic Test

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
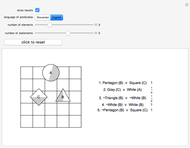
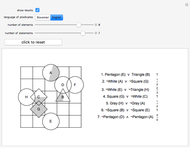
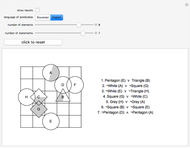
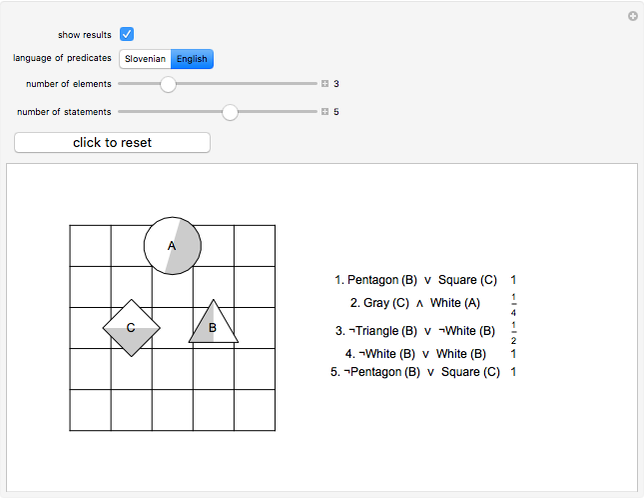
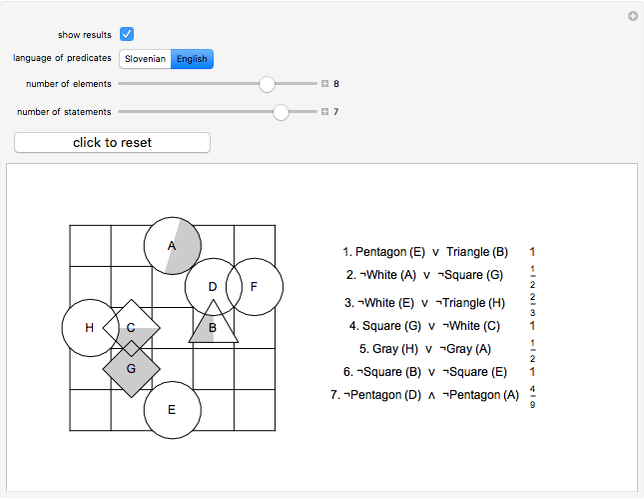
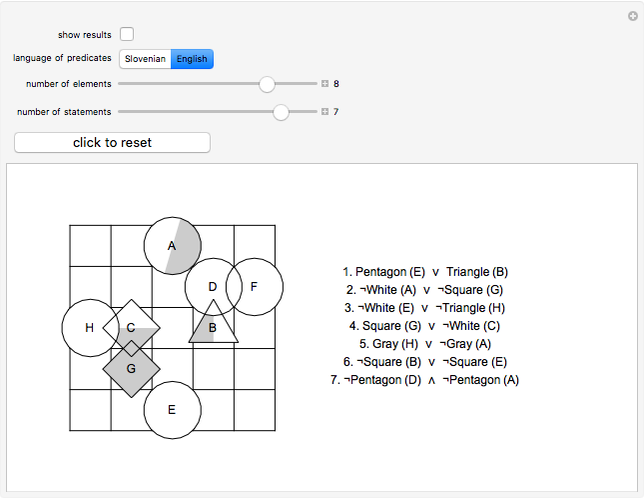
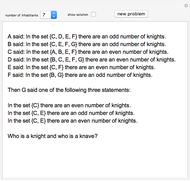
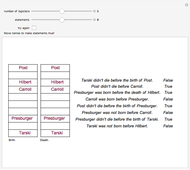
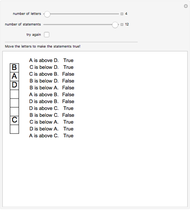
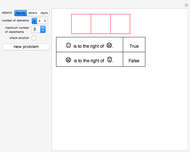
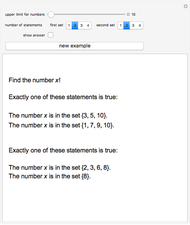
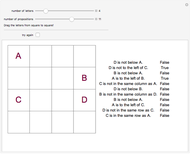
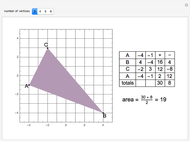
This Demonstration presents a simple test for probability logic. The value of compound propositions is evaluated according to probability laws.
[more]
Contributed by: Izidor Hafner (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
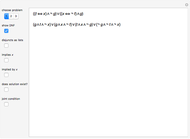
The procedure used should work on any propositional sentence. Using Mathematica's built-in function LogicalExpand eliminates all propositional connectives except ¬, ∧, and ∨. Negation is eliminated by rules, such as 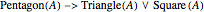 . Another application of LogicalExpand gives a disjunctive normal form without negations, that is a disjunction of conjunctions. There are special cases if the form reduces to a single conjunction, a single atomic statement, or True or False.
. Another application of LogicalExpand gives a disjunctive normal form without negations, that is a disjunction of conjunctions. There are special cases if the form reduces to a single conjunction, a single atomic statement, or True or False.
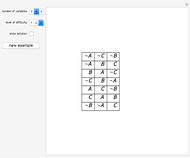
A conjunction is treated as a list of statements 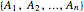 . In case the same figure appears with different shapes or colors, the probability of the conjunction is 0. (For instance:
. In case the same figure appears with different shapes or colors, the probability of the conjunction is 0. (For instance: 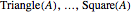 ) If no such case occurs, the set of statements is independent.
) If no such case occurs, the set of statements is independent.
The shape and color of the same figure are independent of each other; the shapes of two different figures are independent, and so on. In these kinds of cases,  and the basic formula for disjunction is
and the basic formula for disjunction is 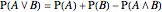 .
.
Permanent Citation