Projectile with Air Drag

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
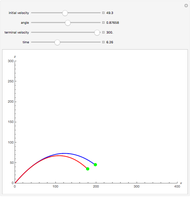
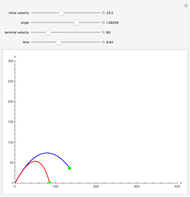
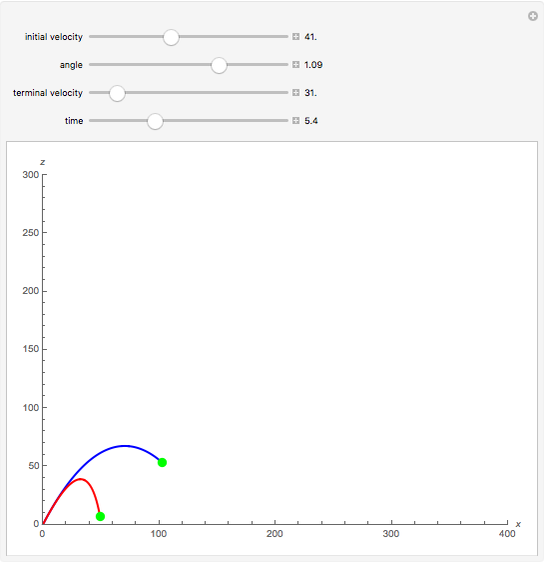
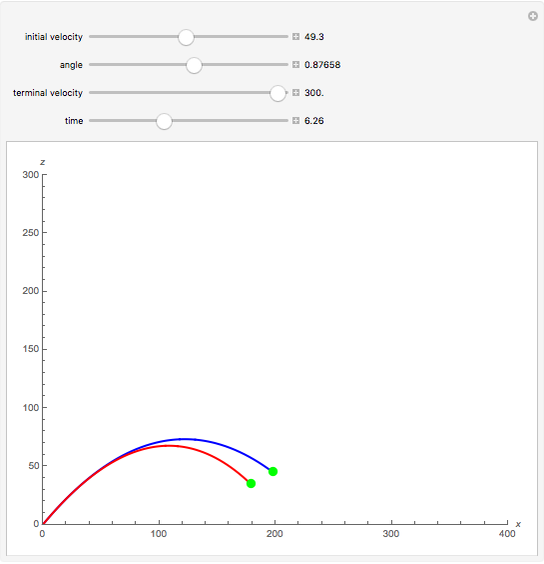
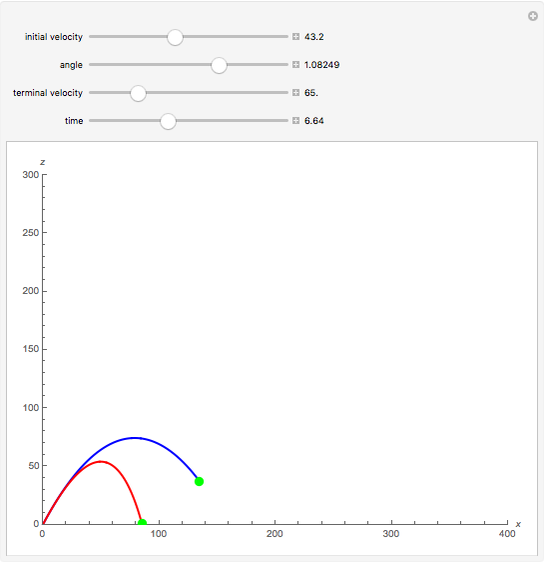
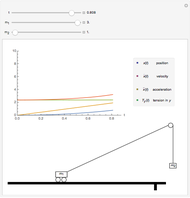
The plots show projectile motion with air resistance (red) compared with the same motion neglecting air resistance (blue). The projectile is launched at an angle  with initial velocity
with initial velocity  . The force due to air resistance is assumed to be proportional to the magnitude of the velocity, acting in the opposite direction.
. The force due to air resistance is assumed to be proportional to the magnitude of the velocity, acting in the opposite direction.
Contributed by: Enrique Zeleny (April 2009)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The equations of motion for the 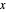 and
and  directions are given by
directions are given by
 ,
,
where  increases upward and
increases upward and  is a positive constant. The terminal velocity is given by
is a positive constant. The terminal velocity is given by 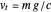 , so the equations can be simplified to
, so the equations can be simplified to
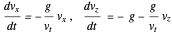 .
.
For a projectile launched at an angle  ,
, 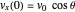 and
and 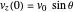 .
.
Integration of the equations of motion gives
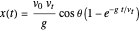 ,
,
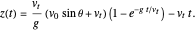
Permanent Citation