Solutions of the Elliptic Membrane Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
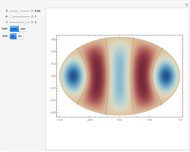
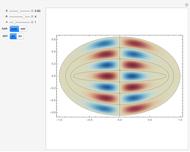
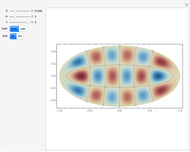
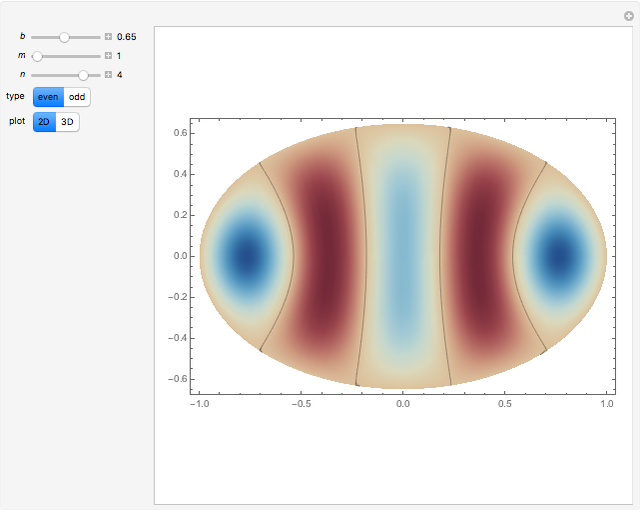
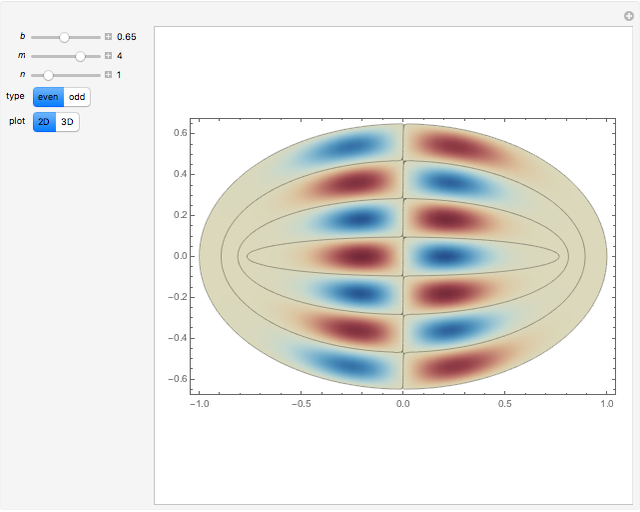
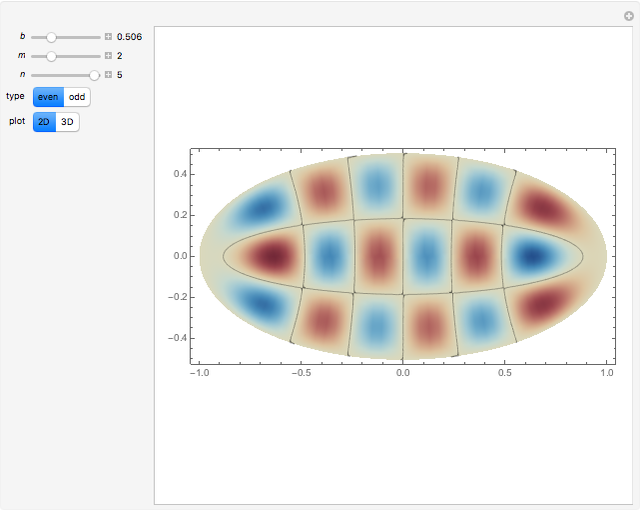
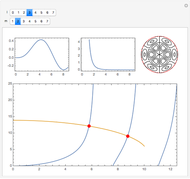
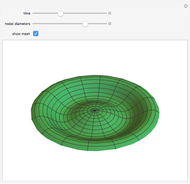
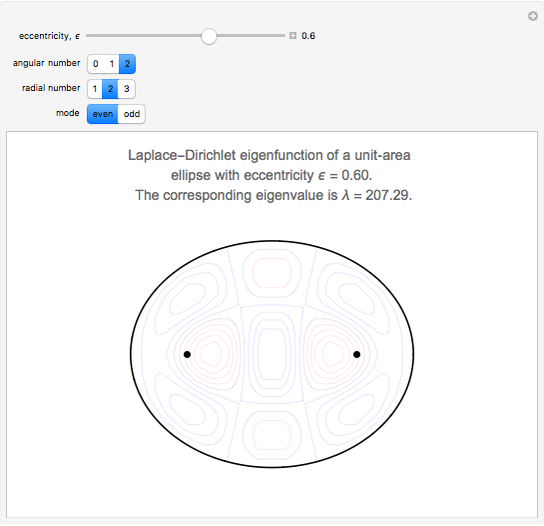
The problem of the free oscillations of an elliptic membrane was studied by Mathieu in 1868. The membrane is anchored to the perimeter of the ellipse. Mathieu functions can appear in problems with elliptical geometry and in certain periodic phenomena.
Contributed by: Enrique Zeleny (November 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Consider the two-dimensional Helmholtz equation

and use elliptic coordinates
 ,
, 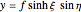
with  (
( is the semiminor axis of the ellipse). Solutions of the type
is the semiminor axis of the ellipse). Solutions of the type  lead to separation of variables, with the pair of differential equations
lead to separation of variables, with the pair of differential equations
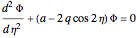 ,
,
 .
.
Now, consider the wave equation
 .
.
Here 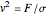 , where
, where 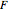 is the tension and
is the tension and  is the surface mass density, and we assume the harmonic dependence
is the surface mass density, and we assume the harmonic dependence  . The wave equation can be rewritten as the Helmholtz equation, with solutions with Dirichlet boundary conditions
. The wave equation can be rewritten as the Helmholtz equation, with solutions with Dirichlet boundary conditions 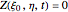 . Thus
. Thus


where  and
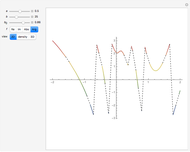
and 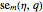 are even and odd angular solutions. These functions are represented in Mathematica as MathieuC[a,q,z] and MathieuS[a,q,z], respectively;
are even and odd angular solutions. These functions are represented in Mathematica as MathieuC[a,q,z] and MathieuS[a,q,z], respectively;  is the characteristic (MathieuCharacteristicA[n,q] and MathieuCharacteristicB[n,q]), a value for which the Mathieu functions are periodic. The radial functions
is the characteristic (MathieuCharacteristicA[n,q] and MathieuCharacteristicB[n,q]), a value for which the Mathieu functions are periodic. The radial functions  and
and  correspond to the same functions with
correspond to the same functions with  . The solutions
. The solutions 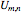 have
have 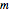 angular nodes and
angular nodes and  radial nodes, with
radial nodes, with  for even modes and
for even modes and  for the odd ones.
for the odd ones.
Reference
[1] J. C. Gutiérrez-Vega, R. M. Rodrı́guez-Dagnino, M. A. Meneses-Nava, and S. Chávez-Cerda, "Mathieu Functions, a Visual Approach," American Journal of Physics, 71(3), 2003 pp. 233–242. doi:10.1119/1.1522698.
Permanent Citation