Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Jorge-Meeks K-Noids

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

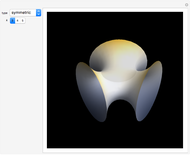
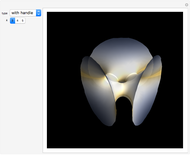
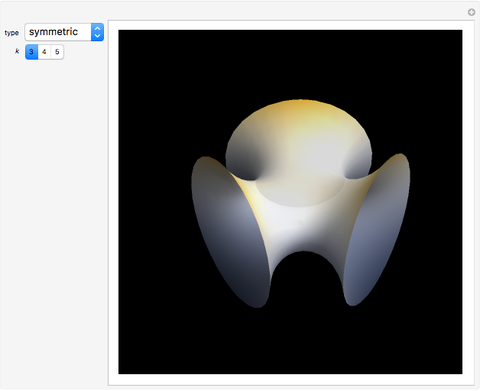
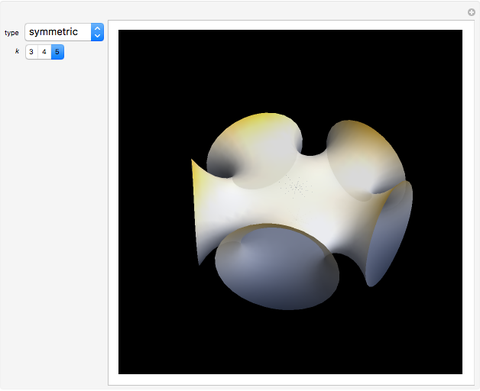
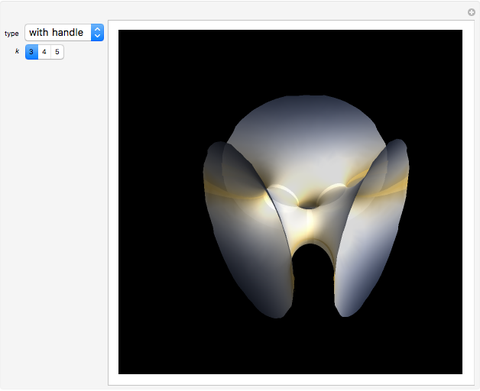
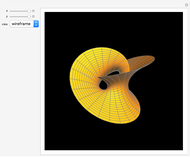
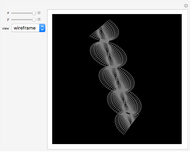
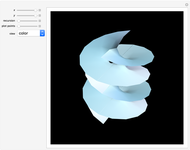
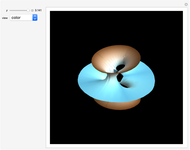
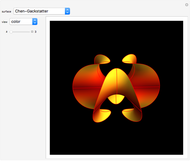
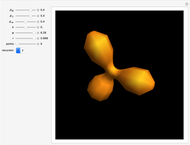
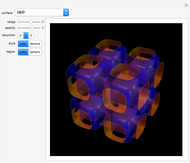
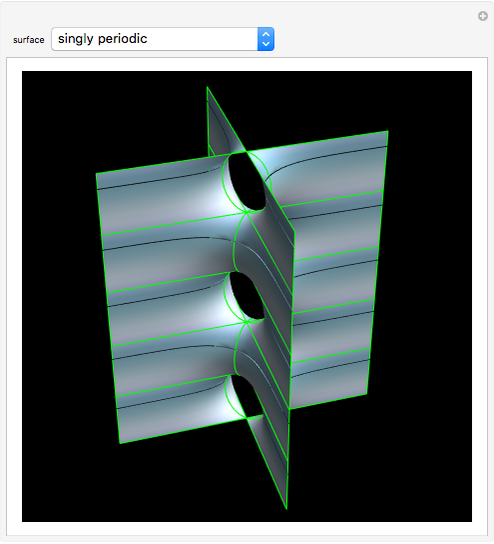
Discovered in 1983, the Jorge and Meeks -noids are complete minimal surfaces of finite total curvature, topologically equivalent to spheres with points removed, positioned with -fold symmetry. The 2-noid is effectively a catenoid and the 3-noid is also known as the trinoid; the -noids are generalizations of the catenoid.

Contributed by: Enrique Zeleny (June 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] L. P. Jorge and W. H. Meeks III, "The Topology of Complete Minimal Surfaces of Finite Total Gaussian Curvature," Topology, 22(2), 1983 pp. 203–221.

[2] M. Weber. "Jorge-Meeks k-Noids." Minimal Surface Archive. (Sep 2013) www.indiana.edu/~minimal/archive/Spheres/Noids/Jorge-Meeks/web/index.html.

[3] H. Karcher, "Construction of Minimal Surfaces," presentation given at Surveys in Geometry (1989), University of Tokyo, 1989. www.math.uni-bonn.de/people/karcher/karcherTokyo.pdf.

[4] U. Dierkes, S. Hildebrandt, and F. Sauvigny, Minimal Surfaces, 2nd ed., New York: Springer, 2010.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send