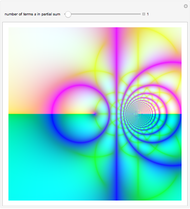
Coulomb Wavefunctions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
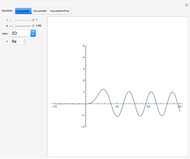
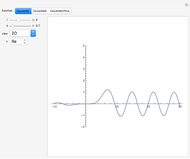
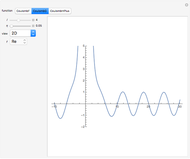
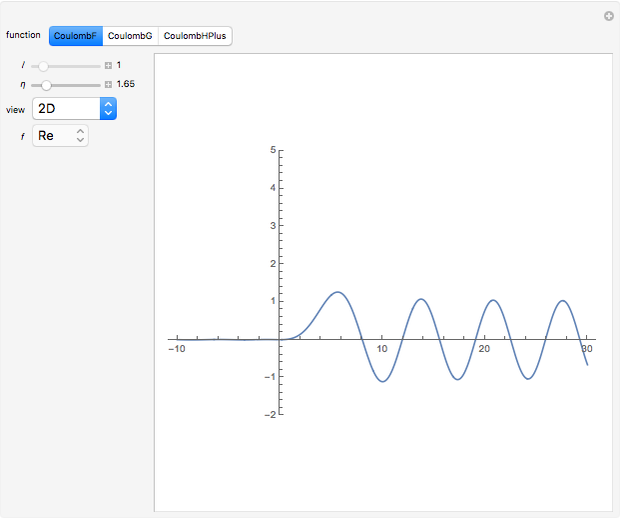
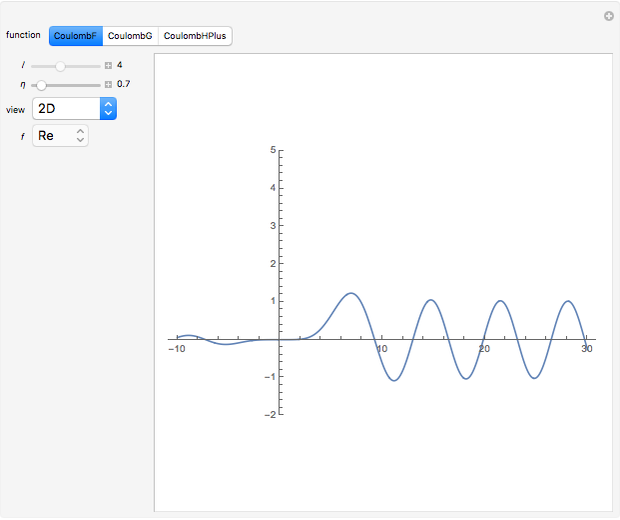
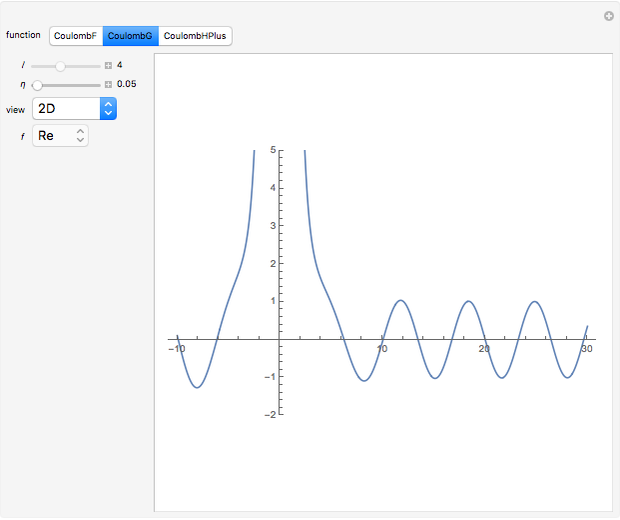
Coulomb wavefunctions are solutions of the Schrödinger equation for scattering of charged particles by a positively charged nucleus, described by a 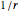 Coulomb potential. They are important for applications in the quantum theory of scattering, particularly for nuclear physics. Coulomb wavefunctions can be expressed in terms of confluent hypergeometric functions or, alternatively, Whittaker functions. Two special solutions, called the regular and irregular Coulomb wavefunctions, according to their analytic behavior at the nucleus, are denoted by
Coulomb potential. They are important for applications in the quantum theory of scattering, particularly for nuclear physics. Coulomb wavefunctions can be expressed in terms of confluent hypergeometric functions or, alternatively, Whittaker functions. Two special solutions, called the regular and irregular Coulomb wavefunctions, according to their analytic behavior at the nucleus, are denoted by 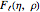 and
and 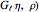 , respectively.
, respectively.
Contributed by: Enrique Zeleny (August 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] L. J. Slater, "Coulomb Wave Functions," Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (M. Abramowitz and I. A. Stegun, eds.), 9th ed., New York: Dover, 1972 pp. 537–544.
[2] I. J. Thompson. "Coulomb Functions." Digital Library of Mathematical Functions. (Apr 25, 2014) dlmf.nist.gov/33.
[3] F. W. J. Olver, D. W. Lozier, R. F. Boisvert, and C. W. Clark, eds., NIST Handbook of Mathematical Functions, New York: Cambridge University Press, 2010.
[4] QuantumDot. "Irregular Confluent Hypergeometric Functions (Spherical Coulomb Wavefunctions)." Mathematica Stack Exchange. (Mar 22, 2013)mathematica.stackexchange.com/questions/22283/irregular-confluent-hypergeometric-functions-spherical-coulomb-wavefunctions.
Permanent Citation
"Coulomb Wavefunctions"
http://demonstrations.wolfram.com/CoulombWavefunctions/
Wolfram Demonstrations Project
Published: August 26 2014