Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

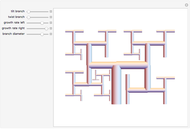
Prüfer Codes of Labeled Trees

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

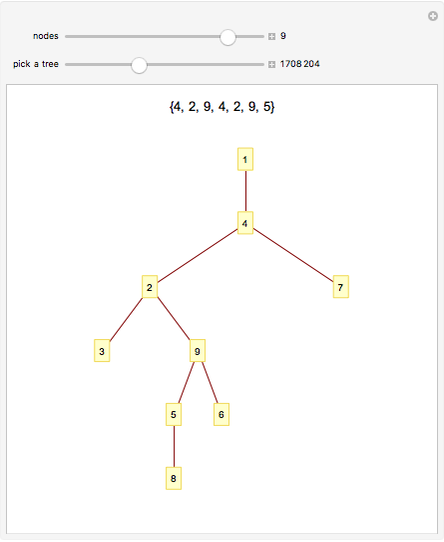
In 1889, Cayley proved that there are 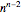labeled trees on nodes. In 1918, Prüfer found a method for constructing each tree.

[more]

Consider the tree with code {2, 8, 9, 4, 7, 7, 2} that is given as the default tree in this Demonstration. The first digit of the Prüfer code is the branch that has the smallest isolated number. Pruning that branch gives a new tree, and the process repeats, as shown in the Details.

[less]

Contributed by: Ed Pegg Jr (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

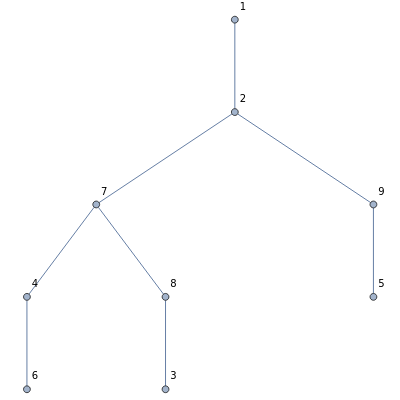
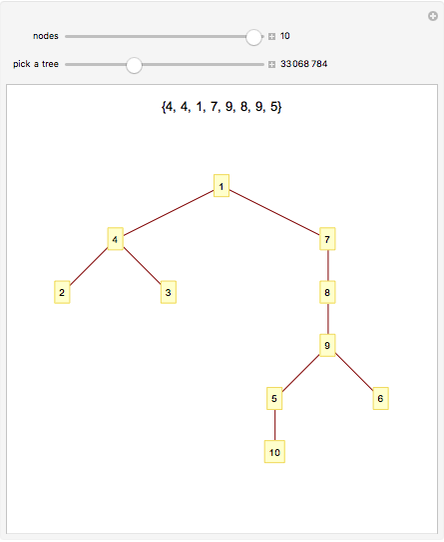
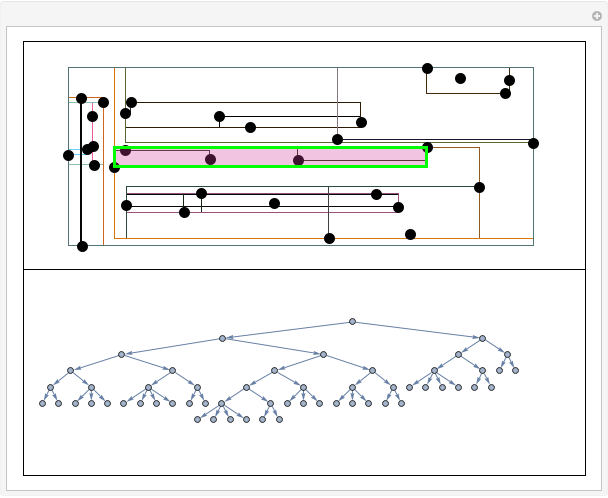
The smallest non-branch number is 1. Cut it from 2. The smallest non-branch number is 3. Cut it from 8. The smallest non-branch number is 5. Cut it from 9. The smallest non-branch number is 6. Cut it from 4. The smallest non-branch number is 4. Cut it from 7. The smallest non-branch number is 8. Cut it from 7. The smallest non-branch number is 7. Cut it from 2.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send