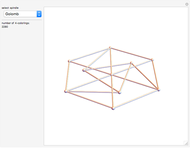
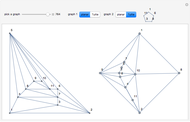
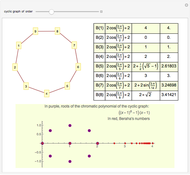
Moser Spindles, Golomb Graphs and Root 33
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
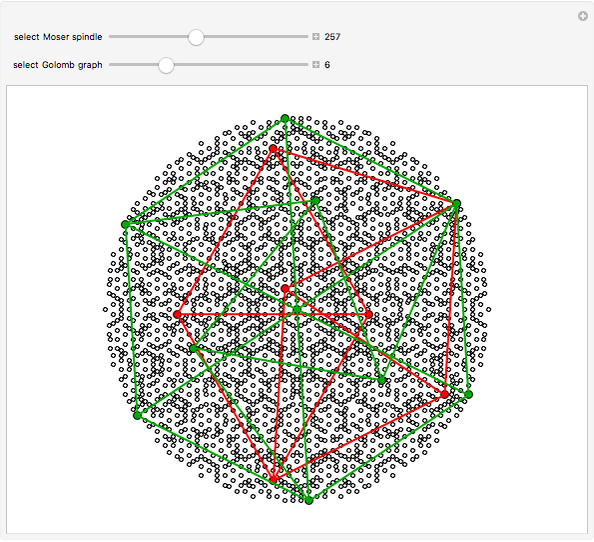
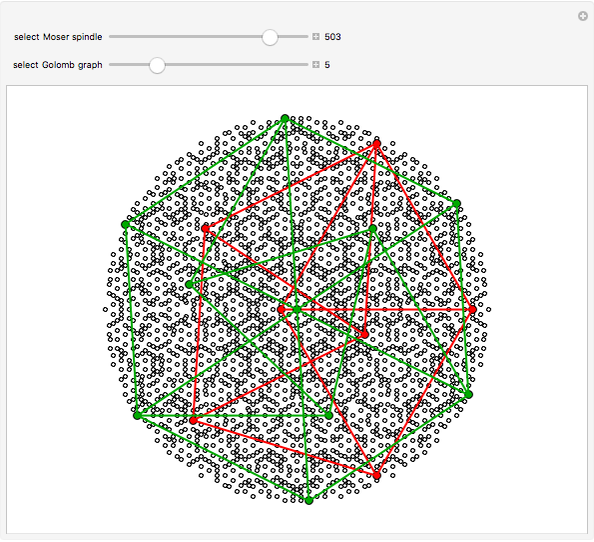
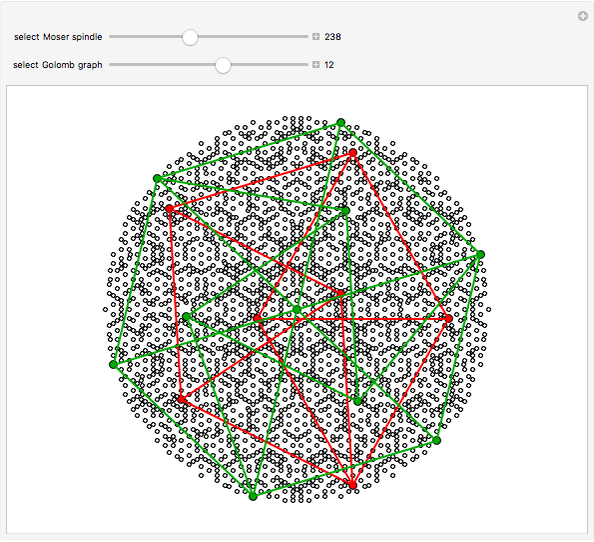
If the plane is divided into  colors, what is the least
colors, what is the least  such that any two points a unit distance apart have different colors? This is the unsolved Hadwiger–Nelson problem, whose answer is 4, 5, 6 or 7 colors.
such that any two points a unit distance apart have different colors? This is the unsolved Hadwiger–Nelson problem, whose answer is 4, 5, 6 or 7 colors.
Contributed by: Ed Pegg Jr (December 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
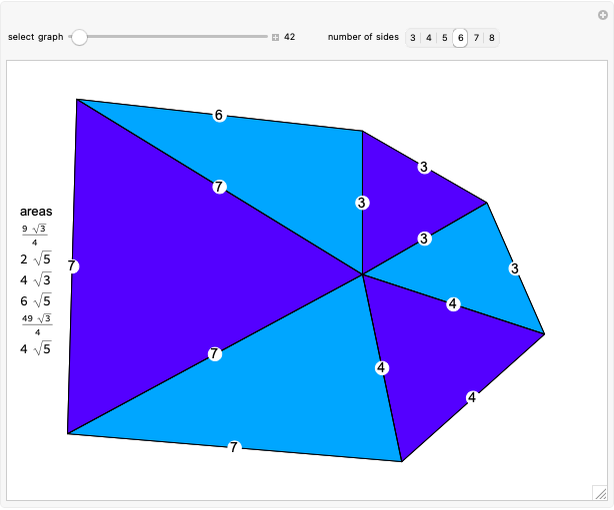
Not all unit distance 4-chromatic graphs are in  . For example, Hochberg–O'Donnell's fish graph has vertices that rely on polynomials of degree 12. An exact solution can be found at the end of the Initialization section.
. For example, Hochberg–O'Donnell's fish graph has vertices that rely on polynomials of degree 12. An exact solution can be found at the end of the Initialization section.
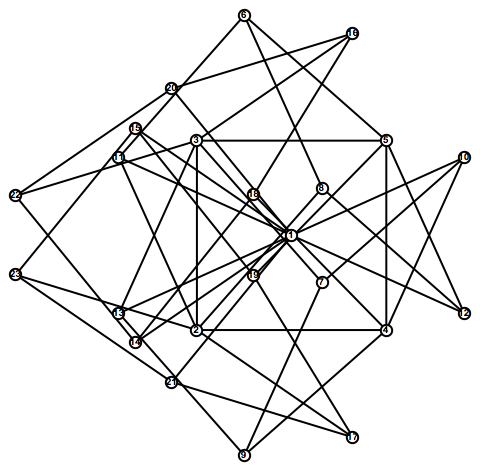
Permanent Citation