Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

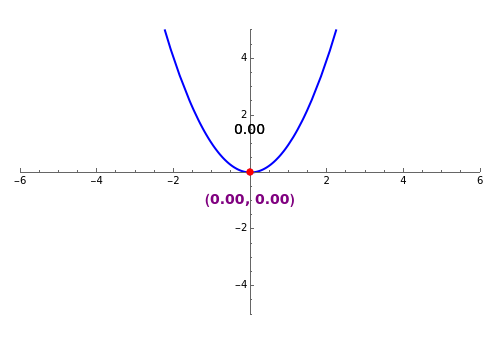
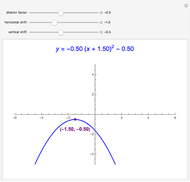
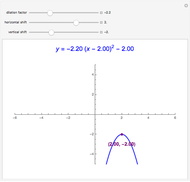
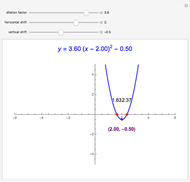
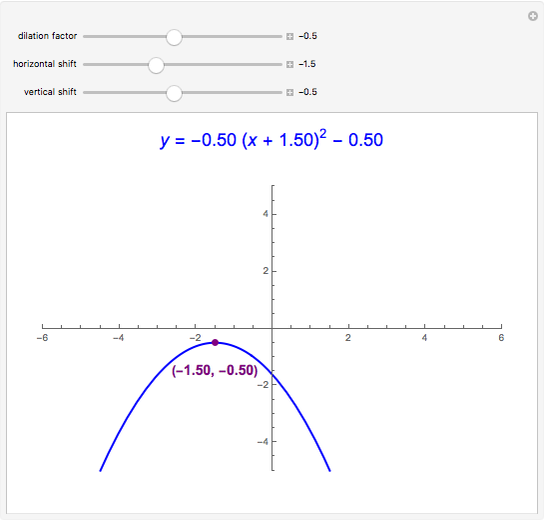
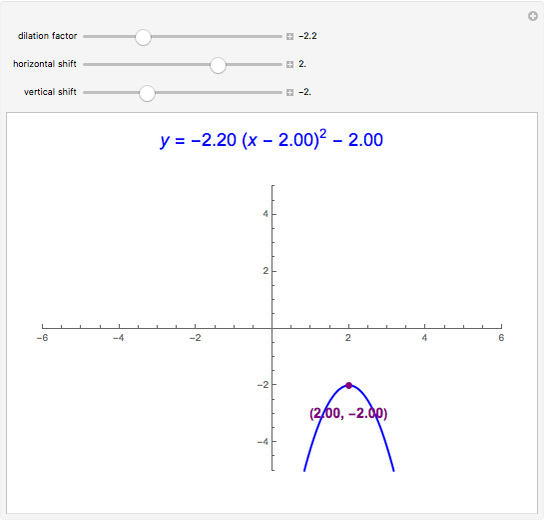
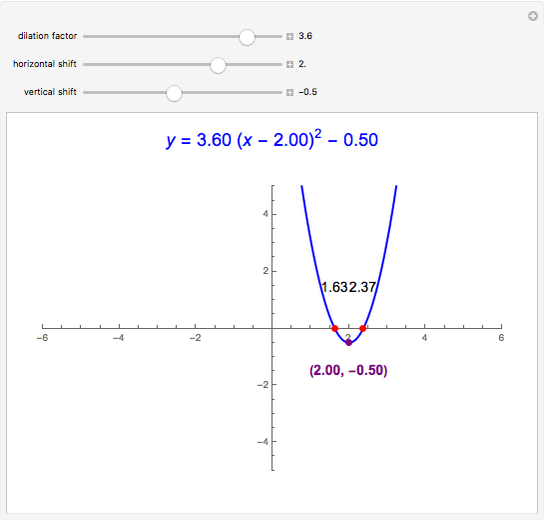
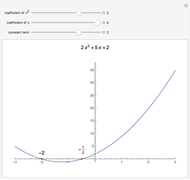
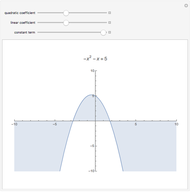
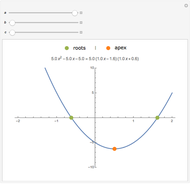
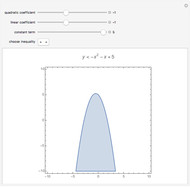
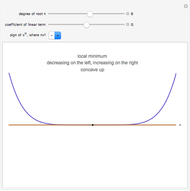
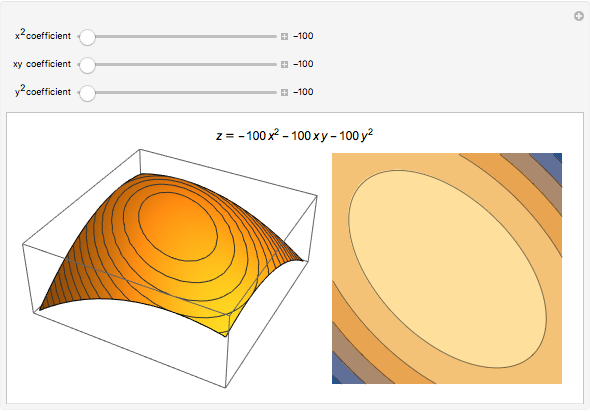
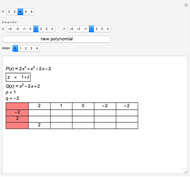
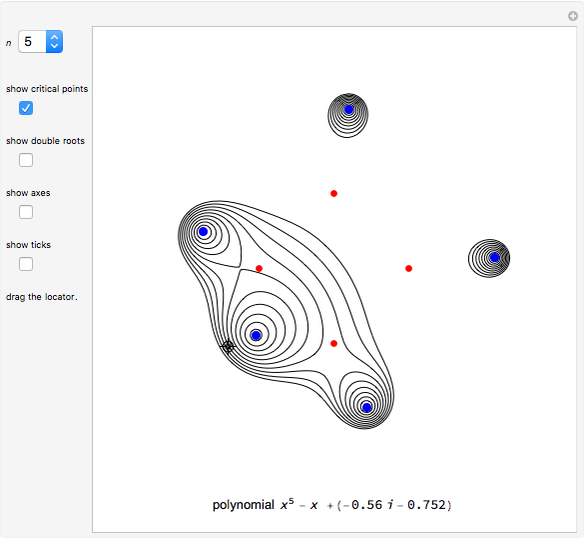
Quadratic in Vertex Form (or Turning Point Form)

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

Expressing a quadratic in vertex form (or turning point form) lets you see it as a dilation and/or translation of 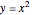. A quadratic in standard form can be expressed in vertex form by completing the square.

Contributed by: Rod Bate (December 2011)
Based on a program by: Stephen Wolfram
Open content licensed under CC BY-NC-SA

Snapshots

Details

Based on Stephen Wolfram's Demonstration "Annotated Quadratic Polynomial".

Reference

[1] Wikipedia. "Quadratic Function." (Nov 28, 2011) en.wikipedia.org/wiki/Quadratic_function.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send