Newton Flows of Polynomials
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
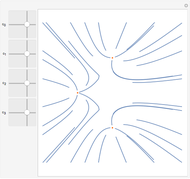
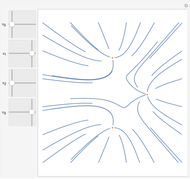
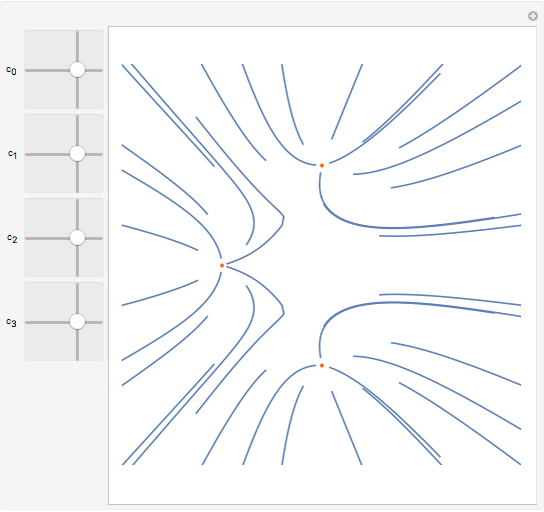
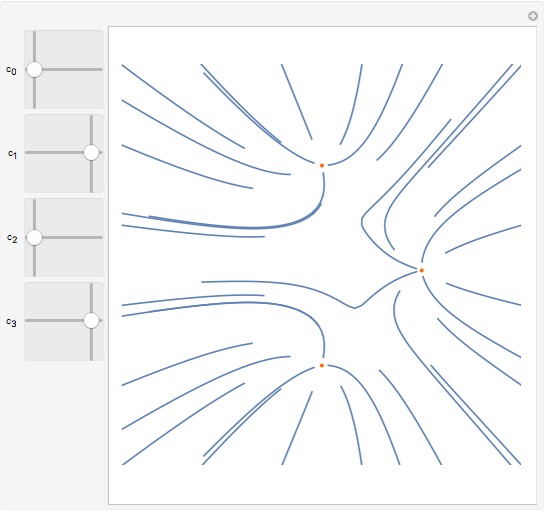
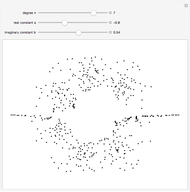
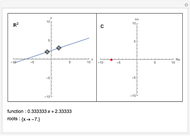
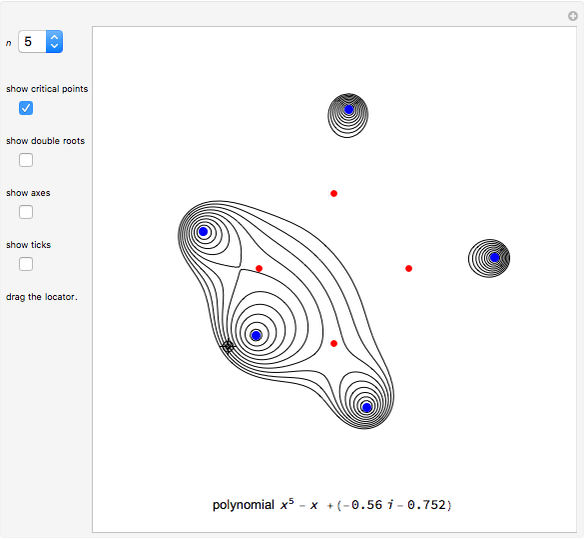
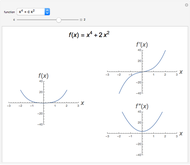
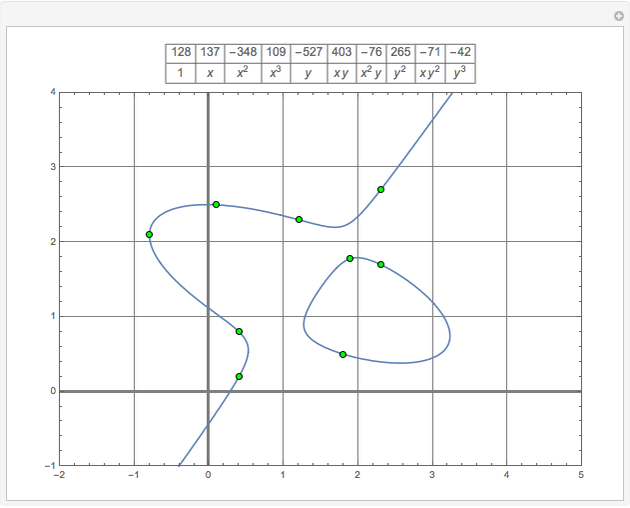
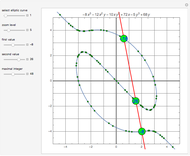
This demonstrates Newton flow of a cubic polynomial. Given a polynomial  , the Newton flow of this polynomial is formed by the solution curves of the differential equation
, the Newton flow of this polynomial is formed by the solution curves of the differential equation 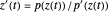 . The red points are the roots of the polynomial.
. The red points are the roots of the polynomial.
Contributed by: Michael Trott (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
 — coefficients of the cubic polynomial
— coefficients of the cubic polynomial 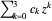
Permanent Citation